Problema
(Indicado a partir do 6º ano do E. F.)
As ruas Canadá e México se encontram formando um T e têm, respectivamente, [tex]480[/tex] m e [tex]360[/tex] m. O cruzamento divide a Rua Canadá em duas partes de mesmo comprimento.
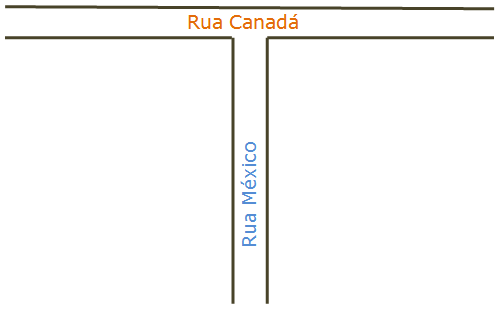
Uma empresa de engenharia planeja colocar postes de iluminação ao longo das ruas de modo que exista um poste em cada extremidade do trecho considerado e um único poste no encontro das duas ruas. É exigido que a distância entre cada dois postes vizinhos seja a mesma e a maior possível. Desconsidere a largura de ambas as ruas.
Qual a quantidade de postes a serem utilizados?
Solução 1
Como é exigido que a distância entre cada dois postes vizinhos seja a mesma e a maior possível e que haja postes no cruzamento e nas extremidades das ruas, a distância padrão entre cada par de postes consecutivos deve dividir tanto [tex]360[/tex] e também [tex]240[/tex].
Então basta calcularmos o [tex]MDC (240, 360)[/tex], pois esta será a maior distância possível entre dois postes vizinhos. O MDC pelo processo das divisões sucessivas é mostrado abaixo.
| 1 | 2 | |
| 360 | 240 | 120 |
| 120 | 0 |
Portanto, [tex]MDC (240, 360) = 120[/tex] e a distância entre os postes deve ser de [tex]120[/tex] metros.
A quantidade total de postes a serem utilizados será
- [tex](480 : 120) + 1 = 5[/tex] na Rua Canadá;
- [tex](360 : 120) + 1 = 4[/tex] na Rua México.
Mas observe que no cruzamento só pode ter um poste, então a quantidade total será [tex]5 + 4 – 1 = 8[/tex] postes.
Há uma maquineta desenvolvida pela Equipe dos Clubes que possibilita o cálculo do MDC.
Para obtê-la, basta clicar AQUI.
Bom estudo.
Solução elaborada pelos Moderadores do Blog.
Solução 2
- Considerando que as distâncias entre os postes devem ser iguais e a maior possível, tiramos o MDC de [tex]360[/tex] (comprimento da Rua do México) e de [tex]240[/tex] (comprimento da Rua do Canadá dividido por dois). O MDC de [tex]360[/tex] e [tex]240[/tex] é [tex]120[/tex]; logo, chegamos à conclusão que a distância entre os postes deve ser de [tex]120 m[/tex].
- Para distribuirmos os postes, dividimos [tex]360[/tex] e [tex]240[/tex] por [tex]120[/tex], o que resultou em [tex]3[/tex] e [tex]2[/tex], respectivamente. Ou seja, na Rua do México precisaríamos de [tex]3[/tex] regiões de [tex]120 m[/tex], o que resultaria em [tex]4[/tex] postes, e na Rua do Canadá de [tex]4[/tex] regiões de [tex]120 m[/tex], o que resultaria em [tex]5[/tex] postes. Como há um poste no cruzamento, que serve tanto para a Rua do México quanto para a Rua do Canadá, desconsideramos [tex]1[/tex] poste.
O que resultaria em [tex]4 + 5 – 1 = 8[/tex] postes no total.
Esta é a distribuição de maneira ilustrada:
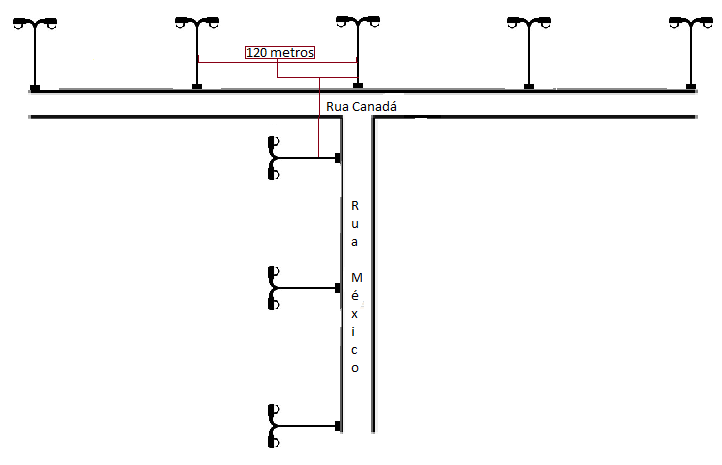
Solução elaborada pelo COM 1uik, com contribuições dos Moderadores do Blog.
Link permanente para este artigo: https://clubes.obmep.org.br/blog/problema-ruas-cruzadas/
