Problema
(Indicado a partir do 9º ano do E. F.)
Uma situação fictícia foi proposta por um professor em uma aula sobre análise de gráficos.
Em um sistema de eixos que está fora de escala, mostrou-se a trajetória de uma bola de pingue-pongue, após a mesma ter sido jogada do alto de um prédio de [tex]100[/tex] metros de altura sobre um piso, suposto irregular.
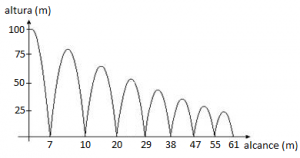
Quantas vezes, ao longo de seu percurso, a bola atingiu a altura de exatamente [tex]30[/tex] metros antes de completar [tex]33,5[/tex] metros de alcance?
Solução 1
Observe a figura abaixo.
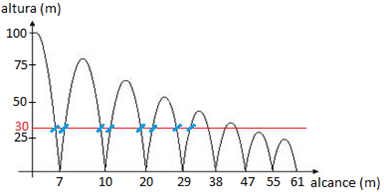
Inicialmente, observe que [tex]33,5[/tex] metros está na metade entre [tex]29[/tex] metros e [tex]38[/tex] metros.
Na figura, os pontos marcados de azul são aqueles onde, antes de completar [tex]33,5[/tex] metros de alcance, a bola alcança a altura [tex]30[/tex] metros, ou seja, exatamente [tex]8[/tex] vezes.
Solução elaborada pelos Moderadores do Blog.
Solução 2
- Inicialmente, observamos visualmente que antes da bola de pingue-pongue alcançar 29m de alcance, ela atinge a altura de 30m sete vezes.
- Sabemos que a distância percorrida pela bolinha na subida é igual à na descida. Como o ponto médio entre 29 e 38m de alcance é 33,5m, concluímos que a bolinha teve altura máxima no alcance de 33,5 entre os alcances de 29 e 38m.
A partir disto, podemos concluir que a bola alcançou 30m mais uma vez, na subida depois dos 29m de alcance.
Assim a bola alcançou a altura de 30m antes de 33,5m de alcance oito vezes.
Solução elaborada pelo COM Águias da Matemátika.
Solução 3
Traçamos uma linha reta na horizontal entre os valores [tex]25[/tex] e [tex]50[/tex].
Com isso, descobrimos que na subida e na descida entre o alcance de [tex]0[/tex] a [tex]33,5 m[/tex], a bola de pingue-pongue passa [tex]8[/tex] vezes na altura de [tex]30[/tex] metros.
O número [tex]8[/tex] foi obtido pelo número de interseções entre a trajetória da bola e a reta horizontal traçada.
Solução elaborada pelo COM MathClub , com contribuições dos Moderadores do Blog.
