Problema
(Indicado a partir do 9º ano do E. F.)
Considere [tex]x, y, z[/tex] algarismos diferentes entre si.
Sendo válida a igualdade [tex]xy+yz+zx=xyz[/tex], na qual [tex]xy[/tex], [tex]yz[/tex], [tex]zx[/tex], [tex]xyz[/tex] são números e não produtos, calcular o valor da expressão [tex]x+y+z[/tex].
Solução 1
● Precisamos lembrar de que se um número natural de dois algarismos é representado como [tex]ab[/tex], então [tex]a[/tex] é o algarismo das dezenas e [tex]b[/tex] o algarismo das unidades.
Dessa forma, [tex]ab=10\cdot a+b[/tex].
● Por outro lado, se um número natural de três algarismos é representado como [tex]abc[/tex], precisamos lembrar que [tex]a[/tex] é o algarismo das centenas, [tex]b[/tex] o algarismo das dezenas e [tex]c[/tex] o algarismo das unidades.
Neste caso, [tex]abc=100\cdot a+10\cdot b+c[/tex].
Com base nessa observação, se [tex]x, \, y, \, z[/tex] são algarismos diferentes entre si, podemos escrever a igualdade
[tex]\qquad \qquad xy+yz+zx=xyz [/tex]
como
[tex]\qquad \qquad [10\cdot x+y]+[10\cdot y+z]+[10\cdot z+x]=100\cdot x+10\cdot y+z[/tex]
e concluir que
[tex]\qquad \qquad y+10\cdot z=89\cdot x[/tex].
Como [tex]x, \, y, \, z[/tex] são algarismos diferentes entre si, o único valor que [tex]x[/tex] pode assumir é [tex]1[/tex], pois os três algarismos não podem ser [tex]0[/tex] e qualquer algarismo maior do que [tex]1[/tex] tornaria [tex]89\cdot x[/tex] um número de três algarismos; o que não pode ocorrer, já que o número formado no primeiro membro da equação pode ter, no máximo, dois algarismos.
Então temos [tex]x=1, \, y=9, \, z=8[/tex] e, portanto, a soma [tex]\boxed{x+y+z=18}[/tex].
Solução elaborada pelos Moderadores do Blog.
Solução 2
Primeiro observamos a conta dada:
[tex]\qquad xy + yz + zx = xyz[/tex]
Para conseguirmos visualizar melhor representamos esta conta de duas formas:
Em pé: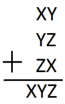
|
Deitada: [tex]\qquad xy + yz+zx= xyz[/tex] |
mas ambas equivalem a
[tex]\qquad 10x + y + 10y + z + 10z + x = 100x + 10y + z[/tex]
Essa igualdade pode ser simplificada até obtermos o resultado [tex] \, 10z + y= 89x[/tex]. Vejamos:
[tex]\qquad 10x + y + 10y + z + 10z + x = 99x + x + 9y + y + z[/tex]
[tex]\qquad 10x + \cancel{y} + 10y + \cancel{z} + 10z + \cancel{x} = 99x + \cancel{x} + 9y + \cancel{y} + \cancel{z}[/tex]
[tex]\qquad 10x + 10y + 10z = 99x + 9y[/tex]
[tex]\qquad 10y + 10z = 89x + 9y[/tex]
[tex]\qquad y + 10z = 89x[/tex]
Utilizando a dica, onde diz que [tex]a + {10}\cdot{b} = ba[/tex], não é maior que [tex]99[/tex], deduzimos que [tex]x[/tex] não pode ser maior que [tex]1[/tex], pois [tex]{89}\cdot{2}[/tex] seria [tex]178[/tex] que já passa de [tex]99[/tex].
Como já sabemos que [tex]x[/tex] é [tex]1[/tex], precisamos agora saber o valor de [tex]y[/tex] e [tex]z[/tex].
Voltando a observar a soma inicial substituindo [tex]x[/tex] por [tex]1[/tex], e como [tex]y[/tex] pode variar de [tex]0[/tex] a [tex]9[/tex], temos:
[tex]\qquad 1+0+z=z+1\le x + y + z\le 1+9+z=z+10[/tex].
Mas também sabemos que o algarismo das unidades de [tex]x + y + z[/tex] é [tex]z[/tex].
Logo, [tex]x + y + z[/tex] é igual a [tex]z + 10[/tex] (notem que é impossível que [tex]z+1,z+2,\cdots,z+9[/tex] possua [tex]z[/tex] como o algarismo das unidades).
Assim,
[tex]\qquad x + y + z = 10 + z[/tex]
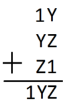Como já sabemos que [tex]x[/tex] é [tex]1[/tex], podemos substituir e descobrir o valor de [tex]y[/tex].
[tex]\qquad\quad 1 + y + z = 10 + z \, \Rightarrow \, 1 + y + \cancel{z} = 10 + \cancel{z}[/tex]
[tex]\qquad\quad 1 + y = 10 \, \Rightarrow \, y = 10 – 1[/tex]
[tex]\qquad\quad y = 9[/tex]
Sendo [tex]y+10=x+y+z+1[/tex] e [tex]x+y=1+9=10[/tex], então [tex]y=z+1[/tex], ou seja [tex]y[/tex] é o algarismo sucessor de [tex]z[/tex]. O antecessor de [tex]9[/tex] é [tex]8[/tex].
Logo [tex]\boxed{x = 1, y = 9, z = 8}[/tex].
Fazendo o teste, podemos confirmar:
[tex]\qquad xy + yz + zx = xyz[/tex]
[tex]\qquad 19 + 98 + 81 = 198[/tex]
A questão diz para calcular [tex]x + y + z[/tex], ou seja, [tex]\boxed{1 + 9 + 8 = 18}[/tex].
Solução elaborada pelo COM 1uik, com contribuições dos Moderadores do Blog.
Link permanente para este artigo: http://clubes.obmep.org.br/blog/probleminha-algarismos-e-numeros/