.Problema: Usando régua e compasso

Problema
(Indicado a partir do 9º ano do E. F.)

Dispondo apenas de um compasso e de uma régua não graduada:
(a) Determine o ponto médio de um dado segmento de reta.
(b) A partir de um quadrado de área [tex]Q[/tex], construir um quadrado de área [tex]\dfrac{Q}{2}[/tex].

Texto de apoio

explicador_p

Brinque um pouco com mediatrizes.

Ajuda

Você já sabe que a circunferência é um lugar geométrico; vejamos outro lugar geométrico.

Definição: A mediatriz de um segmento de reta é a reta perpendicular a ele, traçada pelo seu ponto médio.

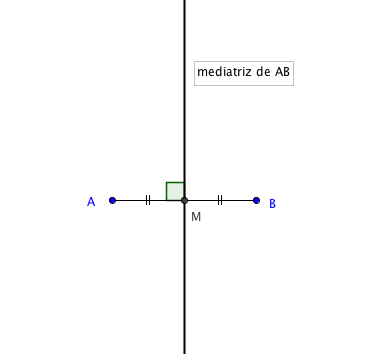
figura 1

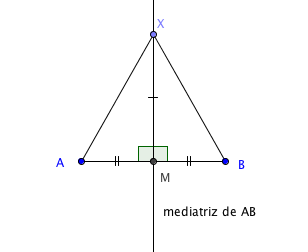
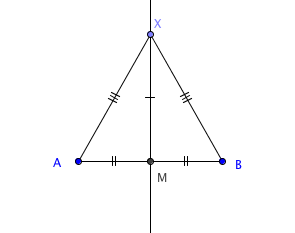
Propriedade importante: A mediatriz de um segmento [tex]\overline{AB}[/tex] é o lugar geométrico dos pontos do plano que equidistam de [tex]A[/tex] e de [tex]B[/tex].

As duas construções que faremos vão se basear fortemente nessa propriedade. Não é necessário que você saiba fazer a demonstração dela para entender as construções; mas se você quiser conhecer a demonstração, basta clicar no botão abaixo.

Prova da propriedade
Dois conjuntos [tex]R[/tex] e [tex]S[/tex] são iguais quando
     (i) todo elemento de [tex]R[/tex] é elemento de [tex]S[/tex]
e
     (ii) todo elemento de [tex]S[/tex] é elemento de [tex]R[/tex].
Seja [tex]S[/tex] a mediatriz do segmento [tex]\overline{AB}[/tex] e [tex]R[/tex] o lugar geométrico dos pontos [tex]X[/tex] do plano tais que [tex]XA = XB[/tex]. Iremos mostrar que [tex]S = R[/tex].

  • Tome um ponto [tex]X[/tex] qualquer da mediatriz; se [tex]X[/tex] é o ponto médio de [tex]\overline{AB}[/tex], que indicaremos por [tex]M[/tex], temos que [tex]X \in R[/tex]. Caso contrário, trace os segmentos [tex]\overline{XA}[/tex] e [tex]\overline{XB}[/tex] e perceba que os triângulos [tex]\Delta XAM[/tex] e [tex]\Delta XBM[/tex] são congruentes pelo caso lado-ângulo-lado e, portanto, [tex]XA = XB[/tex], donde temos [tex]X \in R[/tex]. Assim, todo ponto de [tex]S[/tex] é ponto de [tex]R[/tex].
    figura 2
  • Tome um ponto [tex]X[/tex] qualquer de [tex]R[/tex], ou seja, um ponto tal que [tex]XA = XB[/tex]. Se [tex]X[/tex] é o ponto médio de [tex]\overline{AB}[/tex], temos [tex]X \in S[/tex]. Caso contrário, trace [tex]\overline{XA}[/tex], [tex]\overline{XB}[/tex] e a reta [tex]XM[/tex]; perceba que os triângulos [tex]XAM[/tex] e [tex]XMB[/tex] são congruentes pelo caso lado-lado-lado. Portanto, os ângulos [tex]\angle XMA[/tex] e [tex]\angle XMB[/tex] são congruentes; como são também suplementares, ambos são ângulos retos. Assim a reta [tex]XM[/tex] é a mediatriz de [tex]\overline{AB}[/tex] e [tex]X \in S[/tex]. Portanto todo ponto de [tex]R[/tex] é ponto de [tex]S[/tex].
    figura 3

Concluímos, assim, que [tex]S = R[/tex].
C.Q.D.

Solução

  • Construção (a)
     
    Seja [tex]\overline{AB}[/tex] o segmento de reta dado.
    Como por dois pontos distintos passa uma única reta e a mediatriz de [tex]\overline{AB}[/tex] é o conjunto de todos os pontos do plano que equidistam de [tex]A[/tex] e de [tex]B[/tex] (propriedade enunciada acima), basta encontrarmos dois destes pontos equidistantes de [tex]A[/tex] e de [tex]B[/tex] que a mediatriz será a reta determinada por eles.
     
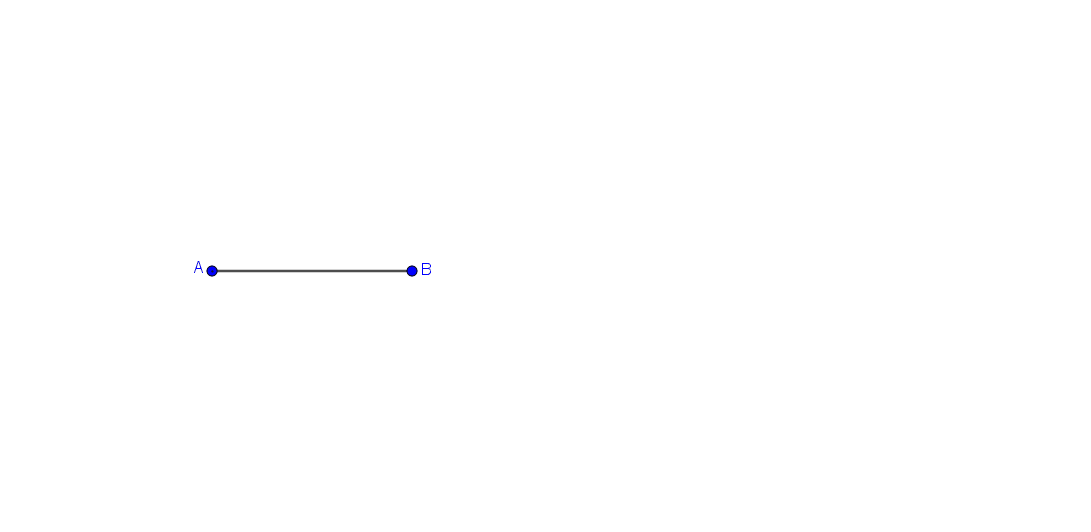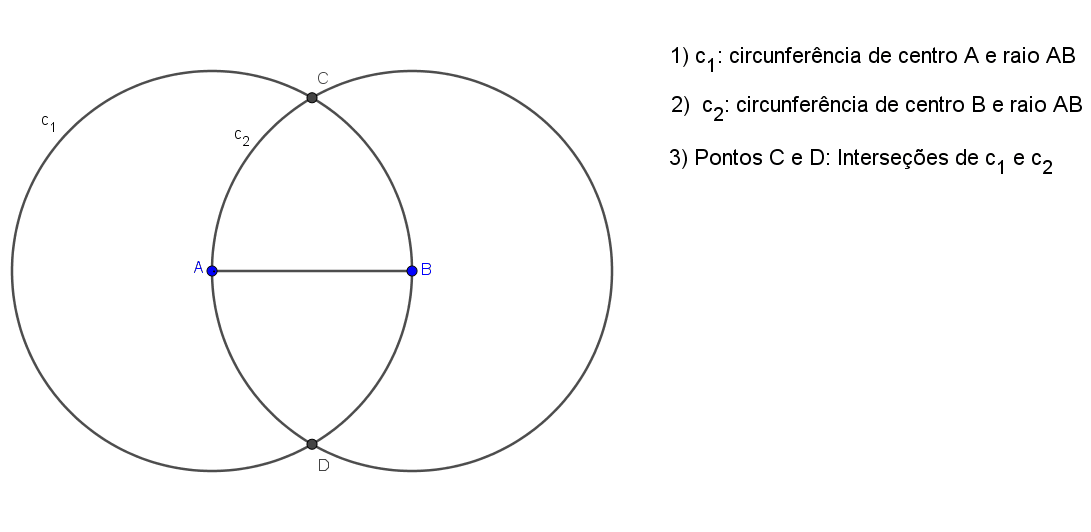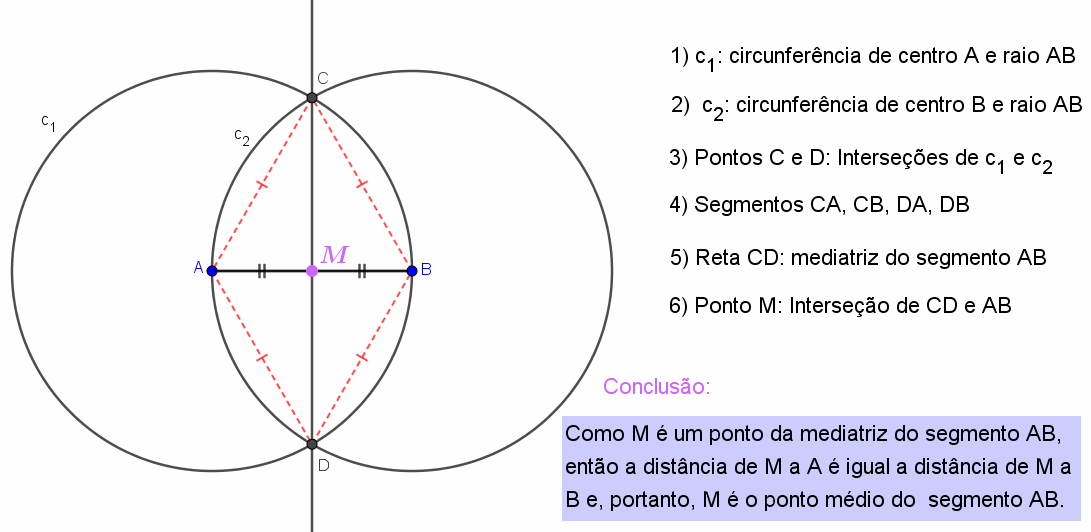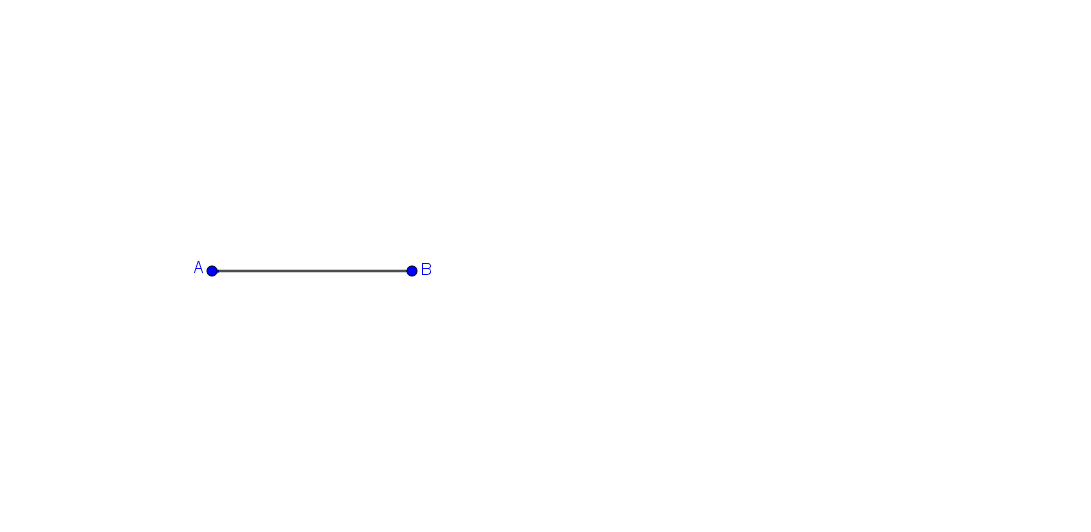
    Passo 1: Com compasso em [tex]A[/tex] e raio [tex]AB[/tex] descrevemos uma circunferência [tex]c_1[/tex].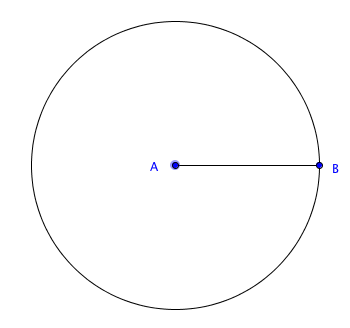

    figura 4

    Passo 2: Com compasso em [tex]B[/tex] e raio [tex]AB[/tex] descrevemos uma circunferência [tex]c_2[/tex].

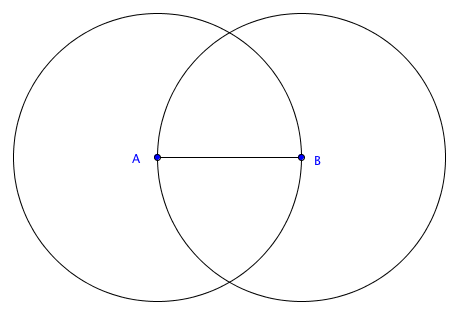
    figura 5

    Passo 3: [tex]c_1[/tex] e [tex]c_2[/tex] se intersectam em dois pontos [tex]C[/tex] e [tex]D[/tex] cujas distancias a [tex]A[/tex] e a [tex]B[/tex] são iguais a [tex]AB[/tex].

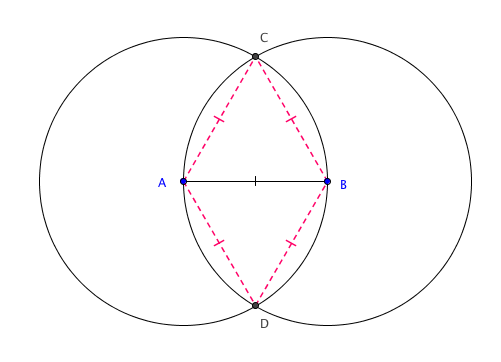
    figura 6

    Passo 4: Com uma régua traçamos a reta [tex]CD[/tex] que será a mediatriz de [tex]\overline{AB}[/tex]. A interseção de [tex]\overline{CD}[/tex] com [tex]\overline{AB}[/tex] é o ponto médio de [tex]\overline{AB}[/tex].

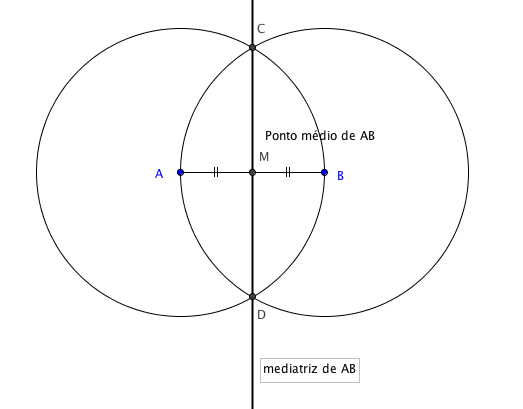
    figura 7

Você pode utilizar um APPLET para fazer a construção que apresentamos ou ver um gif animado. É só clicar no respectivo botão!

Instruções:
Para executar a construção é só esperar o aplicativo carregar completamente e clicar sucessivamente nos quadradinhos que irão aparecer.
Para retornar à configuração inicial, clique nas setinhas que aparecem no canto superior direito do aplicativo.


OBMEP_srg, criado com o GeoGebra

  • Construção (b)

    Considere um quadrado [tex]ABCD[/tex], conforme ilustra a figura abaixo.
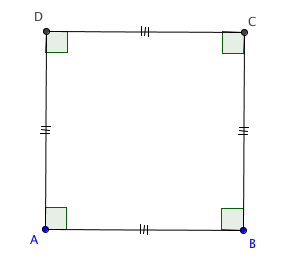
    figura 8
    Passo 1: Determine o ponto médio de cada lado, usando a construção (a).
    Passo 2: Construa o quadrilátero convexo com vértices nos pontos encontrados no Passo 1.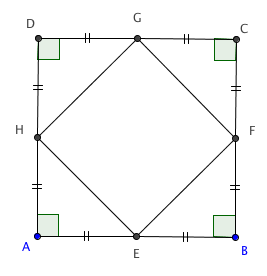

    figura 9

    Afirmação: o quadrilátero construído no Passo 2 é um quadrado de área [tex]\Large \frac{Q}{2}[/tex].

    Prova da afirmação
    Os triângulos [tex]\Delta EBF, \Delta FCG, \Delta GDH \,\text{e}\, \Delta HAE[/tex] são isósceles e congruentes pelo caso lado-ângulo-lado; portanto, os segmentos [tex]\overline{EF}, \overline{FG}, \overline{GH} \,\text{e}\, \overline{HE}[/tex] são congruentes e todos os ângulos destacados em vermelho medem [tex]45^{\circ}[/tex].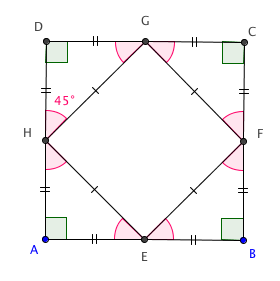

    figura 10

    Sendo [tex]45^{\circ}[/tex] a medida dos ângulos destacados em vermelho, então os ângulos do quadrilátero [tex]EFGH[/tex] são retos; sendo, portanto, [tex]EFGH[/tex] um quadrado.

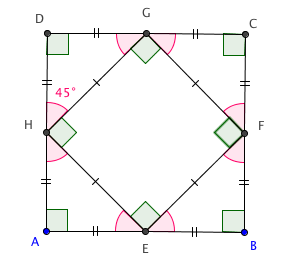
    figura 11

    Finalmente, sendo [tex]a[/tex] a medida dos lados do quadrado [tex]ABCD[/tex], temos [tex]Q = a^2[/tex]. Ao aplicarmos o teorema de Pitágoras num dos triângulos da figura anterior, obtemos que o novo quadrado [tex]EFGH[/tex] tem lado [tex]\dfrac{a\sqrt{2}}{2}[/tex] e, portanto, tem área [tex]\left(\dfrac{a\sqrt{2}}{2}\right)^2 = \dfrac{a^2}{2} = \dfrac{Q}{2} \, .[/tex]

Você pode utilizar um APPLET para fazer a construção do quadrado [tex]EFGH[/tex] a partir de um quadrado [tex]ABCD[/tex] e comparar as áreas dos dois quadrados em questão para algumas situações particulares. É só clicar no botão abaixo.

Instruções:
Para executar a construção e comparar as áreas é só esperar o aplicativo carregar completamente e clicar sucessivamente nos quadradinhos que irão aparecer.
Para modificar o tamanho do lado AB, clique com o botão esquerdo do mouse no ponto azul que aparecerá no primeiro passo da construção, mantenha o botão do mouse pressionado e mova o ponto sobre o segmento azul. (Se você estiver utilizando um celular ou um tablet, toque levemente no ponto azul e movimente-o.)
Para retornar à configuração inicial, clique nas setinhas que aparecem no canto superior direito do aplicativo.
Observação: Lembre-se de que o GeoGebra fornece valores aproximados e que a visualização de várias situações particulares de um fato matemático não substitui sua demonstração.


OBMEP_srg, criado com o GeoGebra

Solução elaborada pelos Moderadores do Blog

Participou da discussão do problema o Clube Math Error.

Link permanente para este artigo: http://clubes.obmep.org.br/blog/problema-usando-regua-e-compasso/