Problema
(Indicado a partir do 9º ano do E. F.)
Um jovem utilizou várias varetas de madeira e construiu, no chão plano de uma quadra, a figura mostrada a seguir.
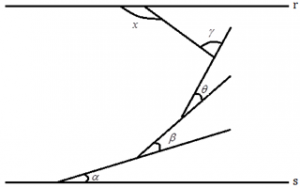
É sabido que as varetas r e s são paralelas e os ângulos indicados foram marcados pelo jovem.
Qual a relação que indica corretamente o valor da medida do ângulo [tex]x[/tex]?
Solução 1
Traçando as retas [tex]t, \, u, \, v[/tex] paralelas às retas [tex]r[/tex] e [tex]s[/tex] conforme mostra a figura abaixo, obtemos os ângulos [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex], adjacentes, respectivamente, aos ângulos iniciais [tex]\beta[/tex], [tex]\theta[/tex] e [tex]\gamma[/tex].
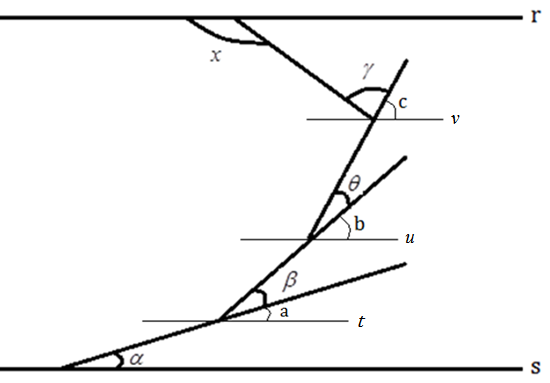
Identificando ângulos com suas respectivas medidas, observamos que,
- considerando as retas paralelas [tex] \, r \, [/tex] e [tex] \, v[/tex], temos que [tex]\boxed{\gamma+c=x}[/tex], pois temos dois ângulos alternos internos.
Além disso,
- observando as retas paralelas [tex] \, u \, [/tex] e [tex] \, v[/tex], temos que [tex]\theta+b=c[/tex], pois agora temos dois ângulos correspondentes.
Dessa forma, [tex]x=\gamma+c=\gamma+\theta+b[/tex], ou seja, [tex]\boxed{x=\gamma+\theta+b}[/tex].
- Analisando as retas paralelas [tex] \, t \, [/tex] e [tex] \, u \, [/tex], notamos que [tex]\beta+a=b[/tex], já que temos, novamente, ângulos correspondentes,
logo [tex]x=\gamma+\theta+b=\gamma+\theta+\beta+a[/tex] e [tex]\boxed{x=\gamma+\theta+\beta+a}[/tex].
Por fim,
- observando as retas paralelas [tex] \, t \, [/tex] e [tex] \, s \, [/tex], concluímos que [tex]a=\alpha[/tex], já que os ângulos são correspondentes.
Portanto, [tex]\fcolorbox{black}{#C6E2FF}{$x=\gamma+\theta+\beta+\alpha$}[/tex].
Solução elaborada pelos Moderadores do Blog.
Solução 2
Primeiramente, traçamos três retas paralelas às retas dadas, nas intersecções das varetas, logo depois fomos destacando os ângulos correspondentes, de baixo para cima.
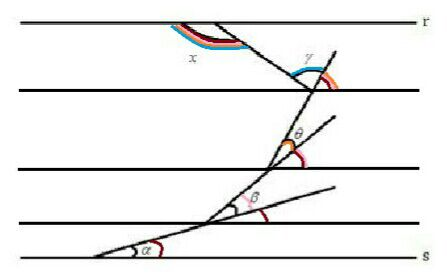
Ao chegar ao ângulo [tex]\gamma[/tex], percebemos que [tex]x[/tex] é a soma dos ângulos [tex]\gamma[/tex] + [tex]\theta[/tex] + [tex]\beta[/tex] + [tex]\alpha[/tex].
Para deixar mais claro, digamos que o ângulo dentro do círculo vermelho seja [tex]y[/tex].
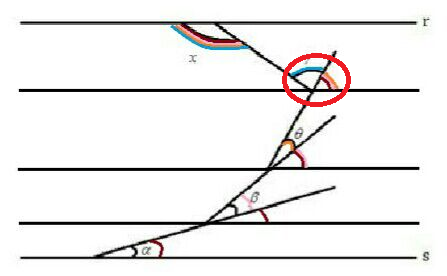
Logo, a justificativa que mostra o valor correto de [tex]x[/tex] é esta: [tex]x[/tex] e [tex]y[/tex] ([tex]\gamma[/tex] + [tex]\theta[/tex] + [tex]\beta[/tex] + [tex]\alpha[/tex]) são ângulos alternos internos, ou seja, têm medidas iguais.
Solução elaborada pelo COM 1uik, com contribuições dos Moderadores do Blog.
