Problema
Um número de cinco algarismos [tex]abcde[/tex] diz-se uma cordilheira se os seus algarismos verificarem as desigualdades [tex] \, \, a \lt b \gt c \lt d \gt e[/tex].
Por exemplo, [tex]37452[/tex] é uma cordilheira.
Quantas cordilheiras existem?
(Aqui, a notação [tex]abcde[/tex] não indicará um produto e sim a representação de um número de cinco algarismos no sistema decimal.)
Solução
Considere uma cordilheira [tex]abcde[/tex].
(1) Observamos, inicialmente, que [tex]a, \, b, \, c, \, d, \, e[/tex] são algarismos; logo podem assumir, apenas, os valores:
[tex]0, \, 1, \, 2, \, 3, \, 4, \, 5, \, 6, \, 7, \, 8, \, 9.[/tex]
(2) Pelas exigências do problema, [tex]c[/tex] é estritamente menor do que [tex] \, b \, [/tex] e [tex] \, d[/tex], assim [tex]c[/tex] não pode ser [tex]9[/tex], caso contrário não teríamos valores para [tex] \, b \, [/tex] e [tex] \, d[/tex]. Assim:
o algarismo central [tex]c[/tex] de uma cordilheira pode variar de [tex]0 \, [/tex] a [tex] \, 8[/tex].
(3) Como já sabemos que [tex]c \, [/tex] é estritamente menor do que [tex]b \, [/tex] e [tex] \, d[/tex], então:
para cada valor de [tex]c[/tex], os algarismos [tex]b \, [/tex] e [tex] \, d[/tex] podem variar de [tex]c+1[/tex] até [tex]9[/tex].
(4) Por outro lado, [tex]a[/tex] é estritamente menor do que [tex]b \, [/tex] e, também, [tex]a\ne 0[/tex], pois a cordilheira tem cinco algarismos. Com isso, para cada valor de [tex]b[/tex], o algarismo [tex]a[/tex] pode variar de [tex]1[/tex] até [tex]b-1[/tex], ou seja:
para cada valor de [tex]b[/tex], existem [tex]b-1[/tex] possibilidades para [tex]a[/tex].
(5) Finalmente, sabemos que [tex]e[/tex] é estritamente menor do que [tex]d[/tex]; portanto, para cada valor de [tex]d[/tex], o algarismo [tex]e[/tex] pode variar de [tex]0[/tex] até [tex]d-1[/tex]. Assim:
para cada valor de [tex]d[/tex], existem [tex]d[/tex] possibilidades para [tex]e[/tex].
Vamos reunir essas informações em um quadro, para ajudar na análise.
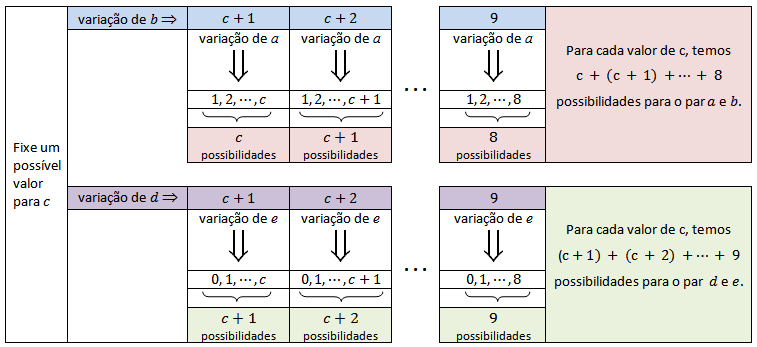
Assim, para um dado valor de [tex]c[/tex] então:
- existem [tex]c + (c + 1) + \dots + 8[/tex] possibilidades para a escolha dos algarismos [tex]a \, [/tex] e [tex] \, b[/tex];
- existem [tex](c + 1) + (c + 2) + \dots + 9[/tex] possibilidades para a escolha dos algarismos [tex]d \, [/tex] e [tex] \, e[/tex].
Dessa forma:
► se [tex]c = 0[/tex], há
[tex]\quad (0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8) × (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9) = 1620[/tex] possibilidades
para os algarismos [tex]a, \, b, \, d, \, e[/tex] (lembre que [tex]a[/tex] não pode ser [tex]0[/tex], por isso aparece um [tex]0[/tex] na primeira parcela do primeiro fator);
► se [tex]c = 1[/tex], há
[tex]\quad (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8) × (2 + 3 + 4 + 5 + 6 + 7 + 8 + 9) = 1584[/tex] possibilidades
para os algarismos [tex]a, \, b, \, d, \, e[/tex];
► se [tex]c = 2[/tex], há
[tex]\quad (2 + 3 + 4 + 5 + 6 + 7 + 8) × (3 + 4 + 5 + 6 + 7 + 8 + 9) = 1470[/tex] possibilidades
para os algarismos [tex]a, \, b, \, d, \, e[/tex];
► se [tex]c = 3[/tex], há
[tex]\quad (3 + 4 + 5 + 6 + 7 + 8)×(4 + 5 + 6 + 7 + 8 + 9) = 1287[/tex] possibilidades
para os algarismos [tex]a, \, b, \, d, \, e[/tex];
► se [tex]c = 4[/tex], há
[tex]\quad (4 + 5 + 6 + 7 + 8) × (5 + 6 + 7 + 8 + 9) = 1050[/tex] possibilidades
para os algarismos [tex]a, \, b, \, d, \, e[/tex];
► se [tex]c = 5[/tex], há
[tex]\quad (5 + 6 + 7 + 8) × (6 + 7 + 8 + 9) = 780[/tex] possibilidades
para os algarismos [tex]a, \, b, \, d, \, e[/tex];
► se [tex]c = 6[/tex], há
[tex]\quad (6 + 7 + 8) × (7 + 8 + 9) = 504[/tex]
possibilidades para os algarismos [tex]a, \, b, \, d, \, e[/tex];
► se [tex]c = 7[/tex], há
[tex]\quad (7 + 8) × (8 + 9) = 255[/tex] possibilidades
para os algarismos [tex]a, \, b, \, d, \, e[/tex];
► se [tex]c = 8[/tex], há
[tex]\quad 8 × 9 = 72[/tex] possibilidades
para os algarismos [tex]a, \, b, \, d, \, e[/tex].
Portanto, como
ou [tex]c = 0[/tex], ou [tex]c = 1[/tex], ou [tex]c = 2[/tex], ou [tex]c = 3[/tex], ou [tex]c = 4[/tex], ou [tex]c = 5[/tex], ou [tex]c = 6[/tex], ou [tex]c = 7[/tex], ou [tex]c = 8[/tex],
existem
[tex]\boxed{1620 + 1584 + 1470 + 1287 + 1050 + 780 + 504 + 255 + 72 = 8622}[/tex] cordilheiras.
Solução elaborada pelos Moderadores do Blog.
Final – Categoria B
10º/12º anos
