Problema
O ângulo [tex]A[/tex] do triângulo isósceles [tex]ABC[/tex] mede [tex]2/5[/tex] de um ângulo reto, sendo iguais seus ângulos [tex]B[/tex] e [tex]C[/tex].
A bissetriz do ângulo [tex]B[/tex] corta o seu lado oposto no ponto [tex]D[/tex].
(a) Calcular as medidas dos ângulos do triângulo [tex]BCD[/tex].
(b) Expressar a medida do lado [tex]\overline{CB}[/tex] em função da medida [tex]b[/tex] do lado [tex]\overline{AB}[/tex], sem que na expressão apareçam razões trigonométricas.
Solução
(a) Pelos dados do problema, inicialmente, observamos que no triângulo [tex]ABC[/tex]:
- o ângulo [tex]A[/tex] mede [tex]\dfrac{2}{5}[/tex] de um ângulo reto, logo mede [tex]\dfrac{2}{5}\times 90^{\circ}=36^{\circ}[/tex];
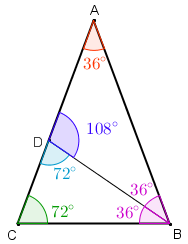
- consequentemente, os ângulos [tex]B \, [/tex] e [tex] \, C[/tex] medem [tex]72^{\circ}[/tex] cada um.
Mas [tex]\overline{BD}[/tex] é a bissetriz do triângulo [tex]ABC[/tex], relativa ao ângulo [tex]B[/tex]; assim,
- os ângulos [tex]A\hat{B}D \, [/tex] e [tex] \, D\hat{B}C[/tex] medem [tex]36^{\circ}[/tex] cada um.
A partir dessa última informação, conseguimos definir as duas medidas que faltam dos ângulos
dos triângulos [tex]ABD \, [/tex]e [tex] \, BCD[/tex]:
- o ângulo [tex]B\hat{D}C[/tex] mede [tex]180^{\circ}-72^{\circ}-36^{\circ}=72^{\circ}[/tex] e o ângulo [tex]B\hat{D}A[/tex]
mede [tex]180^{\circ}-36^{\circ}-36^{\circ}=108^{\circ}[/tex].
A figura ao lado mostra as medidas solicitadas neste item.
(b) Pelo até agora exposto, observamos que os triângulos [tex]BCD[/tex] e [tex]DAB[/tex] são isósceles, além do que os triângulos [tex]ABC[/tex] e [tex]BCD[/tex] são semelhantes.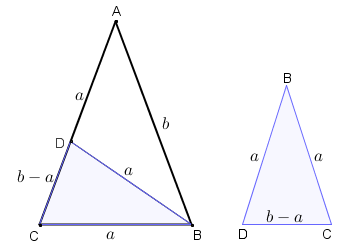
Suponhamos que [tex]a[/tex] seja o comprimento do lado [tex]\overline{CB}[/tex], assim:
- o lado [tex]\overline{BD}[/tex] tem comprimento [tex]a[/tex];
- o lado [tex]\overline{DA}[/tex] tem comprimento [tex]a[/tex];
- o lado [tex]\overline{DC}[/tex] tem comprimento [tex]b-a[/tex];
Como os triângulos [tex]ABC[/tex] e [tex]BCD[/tex] são semelhantes, temos que:
[tex]\qquad \dfrac{b}{a}=\dfrac{a}{b-a}[/tex],
donde
[tex]\qquad a^2+ba-b^2=0[/tex].
Observe, então, que [tex]a[/tex] é uma raiz positiva da equação [tex]x^2+bx-b^2=0[/tex]. Mas as raízes dessa equação são assim obtidas:
[tex]\qquad x=\dfrac{-b\pm\sqrt{b^2+4b^2}}{2}=\dfrac{-b\pm\sqrt{5b^2}}{2}[/tex],
portanto as raízes são [tex]x_1=\dfrac{-b+\sqrt{5b^2}}{2} \, [/tex] e [tex] \, x_2=\dfrac{-b-\sqrt{5b^2}}{2}[/tex].
Sendo [tex]a[/tex] um número positivo, segue que
[tex]\qquad a=\dfrac{-b+\sqrt{5b^2}}{2}=\dfrac{\sqrt{5b^2}-b}{2}[/tex].
Assim, [tex]\boxed{a=\dfrac{b\left(\sqrt{5}-1\right)}{2}}[/tex].
Solução elaborada pelos Moderadores do Blog.
Primera sesión
Fase Nacional
