Problema
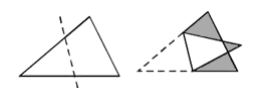
Um triângulo é dobrado ao longo da linha tracejada, de modo a se obter a figura abaixo, cujo contorno é um heptágono.
- A área do triângulo original é 1,5 vezes o valor da área do heptágono.
- A área total das três regiões sombreadas é 1.
Qual é a área do triângulo original?
Solução 1
Só para “desbitolar“, vamos resolver o problema sem utilizar calculadoras e, também, sem o uso de razões como representação de números racionais.
Sejam [tex]H[/tex], [tex]Q[/tex] e [tex]T[/tex] as áreas do heptágono, do quadrilátero branco e do triângulo original, respectivamente.
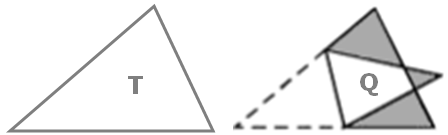
Podemos observar que:
- pela figura da direita, a área do heptágono é a área do quadrilátero branco mais a área sombreada.
Como a área sombreada é [tex]1[/tex], então:
[tex]\qquad H = Q +1. \qquad\qquad (i)[/tex] - pela figura da direita, a área do triângulo original (figura da esquerda) é a área do heptágono mais a área do quadrilátero branco.
Assim:
[tex]\qquad T = H + Q. \qquad\qquad (ii)[/tex] - Pelo enunciado do problema, a área do triângulo original é 1,5 vezes o valor da área do heptágono, logo:
[tex]\qquad T=1,5 \times H. \qquad\qquad (iii)[/tex]
Substituindo [tex](iii)[/tex] em [tex](ii)[/tex], segue que [tex]1,5 \times H = H + Q[/tex] e, assim, obtemos uma quarta equação:
[tex]\qquad 0,5 \times H = Q. \qquad\qquad (iv)[/tex]
Substituindo [tex](iv)[/tex] em [tex](i)[/tex], temos que [tex]H = 0,5 \times H +1[/tex], donde [tex]H=\dfrac{1}{0,5}[/tex].
Agora, substituindo o valor de [tex]H[/tex] em [tex](iii)[/tex], obtemos, finalmente, o valor de [tex]T[/tex]:
[tex]\qquad T=\dfrac{1,5}{0,5}=\dfrac{0,5}{0,5}+\dfrac{0,5}{0,5}+\dfrac{0,5}{0,5}=3[/tex].
Assim, a área do triângulo original equivale a [tex]3 \, unidades \, de \, \acute{a}rea[/tex].
Solução elaborada pelos Moderadores do Blog.
Solução 2
Esta é, provavelmente, a solução feita pela maioria dos que solucionaram o problema.
Sejam [tex]H[/tex], [tex]Q[/tex] e [tex]T[/tex] as áreas do heptágono, do quadrilátero branco e do triângulo original, respectivamente.

Podemos observar que:
- pela figura da direita, a área do heptágono é a área do quadrilátero branco mais a área sombreada.
Como a área sombreada é [tex]1[/tex], então:
[tex]\qquad H = Q +1. \qquad\qquad (i)[/tex] - pela figura da direita, a área do triângulo original (figura da esquerda) é a área do heptágono mais a área do quadrilátero branco.
Assim:
[tex]\qquad T = H + Q. \qquad\qquad (ii)[/tex] - Pelo enunciado do problema, a área do triângulo original é 1,5 vezes o valor da área do heptágono, logo:
[tex]\qquad T=\dfrac{3H}{2}. \qquad\qquad (iii)[/tex]
Substituindo [tex](iii)[/tex] em [tex](ii)[/tex], segue que [tex]\dfrac{3H}{2} = H + Q[/tex] e, assim, obtemos uma quarta equação:
[tex]\qquad Q=\dfrac{H}{2}. \qquad\qquad (iv)[/tex]
Substituindo [tex](iv)[/tex] em [tex](i)[/tex], temos que [tex]H = \dfrac{H}{2} +1[/tex], donde [tex]\dfrac{H}{2}=1[/tex], ou ainda, [tex]H=2[/tex].
Agora, substituindo o valor de [tex]H[/tex] em [tex](iii)[/tex], obtemos, finalmente, o valor de [tex]T[/tex]:
[tex]\qquad T=\dfrac{6}{2}=3[/tex].
Assim, a área do triângulo original equivale a [tex]3 \, unidades \, de \, \acute{a}rea[/tex].
Solução elaborada pelos Moderadores do Blog.
Nível J – 1ª e 2ª séries
