Problema
(Indicado a partir do 1º ano do E. M.)
Num triângulo equilátero de lado [tex]a[/tex], traçamos três arcos de circunferência (no interior do triângulo), cada um com centro num vértice e passando nos pontos médios de dois lados.
Calcule a área da região limitada pelos três arcos.
Solução
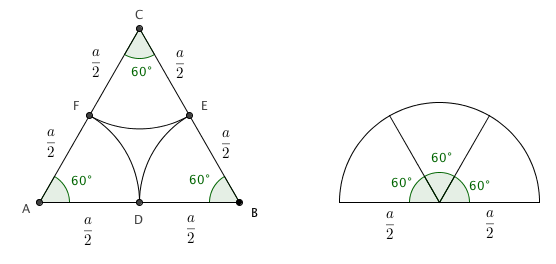
Observe que, após traçarmos os arcos, o triângulo é dividido na região cuja área buscamos e em três setores circulares. Os três setores possuem raios medindo [tex]\dfrac{a}{2}[/tex] e ângulos centrais de [tex]60^\circ[/tex].
Perceba que podemos formar um semicírculo pela junção dos três setores, logo a área [tex]A[/tex] da região limitada pelos arcos é a área do triângulo equilátero de lado [tex]a[/tex] menos a área do semicírculo de raio [tex]\dfrac{a}{2}[/tex].
Portanto,
[tex]\qquad\qquad A = \dfrac{a^2 \cdot \sqrt{3}}{4}-\dfrac{\pi}{2} \cdot \left( \dfrac{a}{2} \right)^2 = \dfrac{2\sqrt{3}-\pi}{8} a^2\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
Aparato
Você pode utilizar um applet para testar o resultado em vários triângulos equiláteros.
É só esperar o aplicativo carregar e movimentar horizontalmente o ponto a que aparece na parte inferior do applet para obter vários triângulos equiláteros com os respectivos elementos envolvidos na solução do problema. Para cada triângulo, observe que o valor decimal apresentado no applet está de acordo com a expressão obtida na resolução.
Boa diversão!
OBMEP_ srdg, criado com o GeoGebra
Lembre-se de que o GeoGebra trabalha com arredondamentos e
que a visualização de várias situações particulares de um fato matemático não substitui sua demonstração.
