.Probleminha: Dados na parede

Problema
(Indicado a partir do 7º ano do E. F.)

---

A pilha abaixo foi construída com dados que têm suas faces marcadas com pontos de [tex]2[/tex] a [tex]7[/tex].
Sabendo que somando os pontos de duas faces opostas quaisquer de qualquer um desses dados o resultado será sempre o mesmo, qual é a soma dos pontos voltados para a parede?

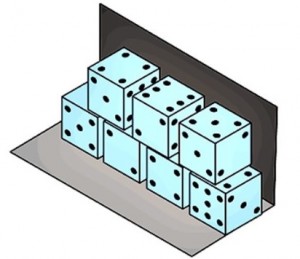
Solução

---

e o dado tem [tex]6[/tex] faces e o que se quer saber é a soma de duas faces opostas, nós somamos todos os números que aparecem no dado e dividimos pela quantia de pares de faces opostas, porque assim teremos quanto vai dar a soma de duas faces opostas, já que somamos o total de pontos que se pode ter em um dado e dividimos pela quantia de pares de faces opostas que se pode ter em um dado.

• quantia de pares de faces opostas: [tex]3[/tex]
• soma de todos os pontos:[tex]27[/tex]
• [tex]\dfrac{27}{3} = 9[/tex]

Então, concluímos que somando os pontos de quaisquer faces opostas teremos [tex]9[/tex] como resultado. Basta vermos, agora, quais os pontos das faces opostas às faces voltadas para a parede, que são as faces da frente, e fazermos a seguinte conta para cada dado:

• [tex]A:[/tex] quantia de pontos da face da frente.
• [tex]B:[/tex] quantia de pontos da face encostada na parede.
• [tex]9 − A = B[/tex]

Assim, teremos como resultados: [tex]6, \, 7, \, 6,4, \, 7, \, 5 \, [/tex] e [tex] \, 2[/tex].
Então, concluímos que a soma dos pontos das faces viradas para a parede é igual a [tex]37[/tex].

---

Solução elaborada pelo COM Os Nóbregas, com contribuições dos Moderadores do Blog.