Problema
Calcule a seguinte soma:
[tex]\dfrac{1}{1993^{-1993}+1}+\dfrac{1}{1993^{-1992}+1}+\cdots+\dfrac{1}{1993^{-1}+1}+\dfrac{1}{1993^{0}+1}+\\
+\dfrac{1}{1993^1+1}+\cdots+\dfrac{1}{1993^{1992}+1}+\dfrac{1}{1993^{1993}+1}\,.[/tex]
Solução
Inicialmente, observe que
[tex]\quad \begin{align*}\dfrac{1}{1993^{-x}+1}+\dfrac{1}{1993^{x}+1}&=\dfrac{1}{\dfrac{1}{1993^x}+1}+\dfrac{1}{1993^{x}+1}\\
&=\dfrac{1}{\dfrac{1993^x+1}{1993^x}}+\dfrac{1}{1993^{x}+1}\\
&=\dfrac{1993^x}{1993^x+1}+\dfrac{1}{1993^{x}+1}\\
&=\dfrac{1993^x+1}{1993^x+1}\\
&=1 \,.\end{align*}[/tex]
Portanto, somando as parcelas extremas da soma, obtemos [tex]1[/tex], o mesmo ocorrendo para as equidistantes das extremas.
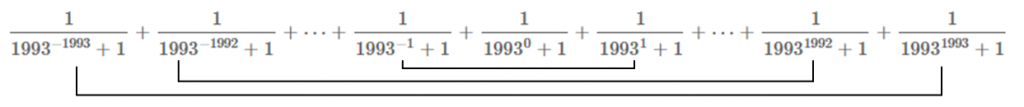
Dessa forma, totalizamos [tex]1993[/tex] parcelas iguais a [tex]1[/tex] e mais a parcela isolada central que é [tex]\dfrac{1}{1993^0+1}=\dfrac{1}{2}[/tex].
Observe:
[tex]\dfrac{1}{1993^{-1993}+1}+\dfrac{1}{1993^{-1992}+1}+\cdots+\dfrac{1}{1993^{-1}+1}+\dfrac{1}{1993^{0}+1}+\dfrac{1}{1993^1+1}+\\
\quad \cdots+\dfrac{1}{1993^{1992}+1}+\dfrac{1}{1993^{1993}+1}=[/tex]
[tex]=\left(\dfrac{1}{1993^{-1993}+1}+\dfrac{1}{1993^{1993}+1} \right)+\left(\dfrac{1}{1993^{-1992}+1}+\dfrac{1}{1993^{1992}+1} \right)+\cdots \\
\quad \cdots + \left(\dfrac{1}{1993^{-1}+1}+\dfrac{1}{1993^{1}+1} \right)+\dfrac{1}{1993^{0}+1}= [/tex]
[tex]=\underbrace{1+1+\cdots + 1}_{1993 \, \, vezes}+\dfrac{1}{2}[/tex].
A soma final será, portanto, [tex]\boxed{1993+\dfrac{1}{2}=1993,5}[/tex].
Solução elaborada pelos Moderadores do Blog.
Categoria B – 10º, 11º e 12º anos
