Problema – Somando distâncias
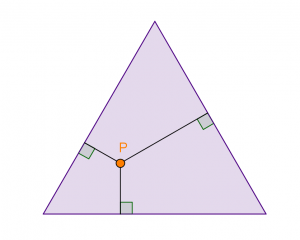
Seja P um ponto no interior de um triângulo equilátero qualquer.
Prove que a soma das distâncias de P aos lados desse triângulo é sempre constante.
Interprete geometricamente o valor desta constante.
 |
Teste a sua solução com o applet abaixo!
|
Testando a solução
Você pode utilizar o applet disponibilizado abaixo para simular diferentes condições iniciais para o problema e, com isso, observar a veracidade da afirmação demonstrada, quantas vezes você quiser!
Para tanto, carregue o applet, escolha um triângulo equilátero e modifique a posição do ponto P.
Lembre-se de que o GeoGebra trabalha com arredondamentos e
que a visualização de várias situações particulares de um fato matemático não substitui sua demonstração.
 |
Para ver uma solução deste problema, clique aqui .
|
Equipe COM – OBMEP
