Problema
Um anel é a região compreendida por dois círculos concêntricos.
Os círculos concêntricos da figura abaixo têm raios com comprimentos [tex]b[/tex] e [tex]c[/tex], com [tex]b\gt c[/tex].
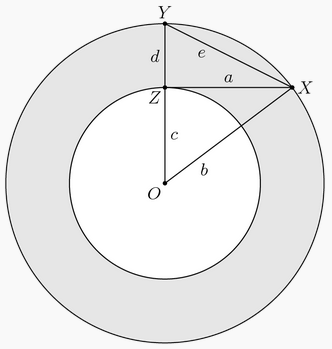
Na figura, [tex]\overline{OX}[/tex] é um dos segmentos que determinam o raio do círculo maior, [tex]\overline{XZ}[/tex] é um segmento tangente ao menor círculo em [tex]Z[/tex] e [tex]\overline{OZ}[/tex] é um dos segmentos que determinam o raio do círculo menor.
Também temos que [tex] \, a \, [/tex] é o comprimento de [tex]\overline{XZ}[/tex], [tex] \, d \, [/tex] é o comprimento de [tex]\overline{YZ}[/tex], [tex] \, e \, [/tex] é o comprimento de [tex]\overline{XY}[/tex].
Então, qual é a área desse anel?
Escreva essa área utilizando a menor expressão possível, ou seja, expresse a área em função de um só comprimento!
Solução
Observe que:
- a área do círculo maior é [tex]\pi b^2[/tex];
- a área do círculo menor é [tex]\pi c^2[/tex];
portanto, a área da região sombreada é [tex]\pi(b^2-c^2)[/tex].
Para melhorar a resposta e escrever a área em função de apenas um dos comprimentos de segmentos apresentados, observe que o triângulo [tex]OXZ[/tex] é retângulo, já que [tex]\overline{XZ}[/tex] é tangente ao menor círculo em [tex]Z[/tex], logo [tex]a^2 + c^2 = b^2[/tex], ou seja, [tex]b^2-c^2=a^2[/tex].
Assim, a área do anel é, também, dada por [tex]\pi a^2[/tex].
Solução elaborada pelos Moderadores do Blog.
Nível B – Questão Média
