Problema
Se um triângulo de área 1 tem lados com comprimentos [tex]a \geq b \geq c[/tex], podemos afirmar que
[tex]\qquad\qquad (a)\,c \geq \sqrt{2}\,\,\,\,\,\,(b)\,b \geq \sqrt{2}\,\,\,\,\,\,(c)\,c \geq 2\,\,\,\,\,\,(d)\,b \geq 2\,\,\,\,\,\,(e)\,N.R.A.[/tex]
Solução
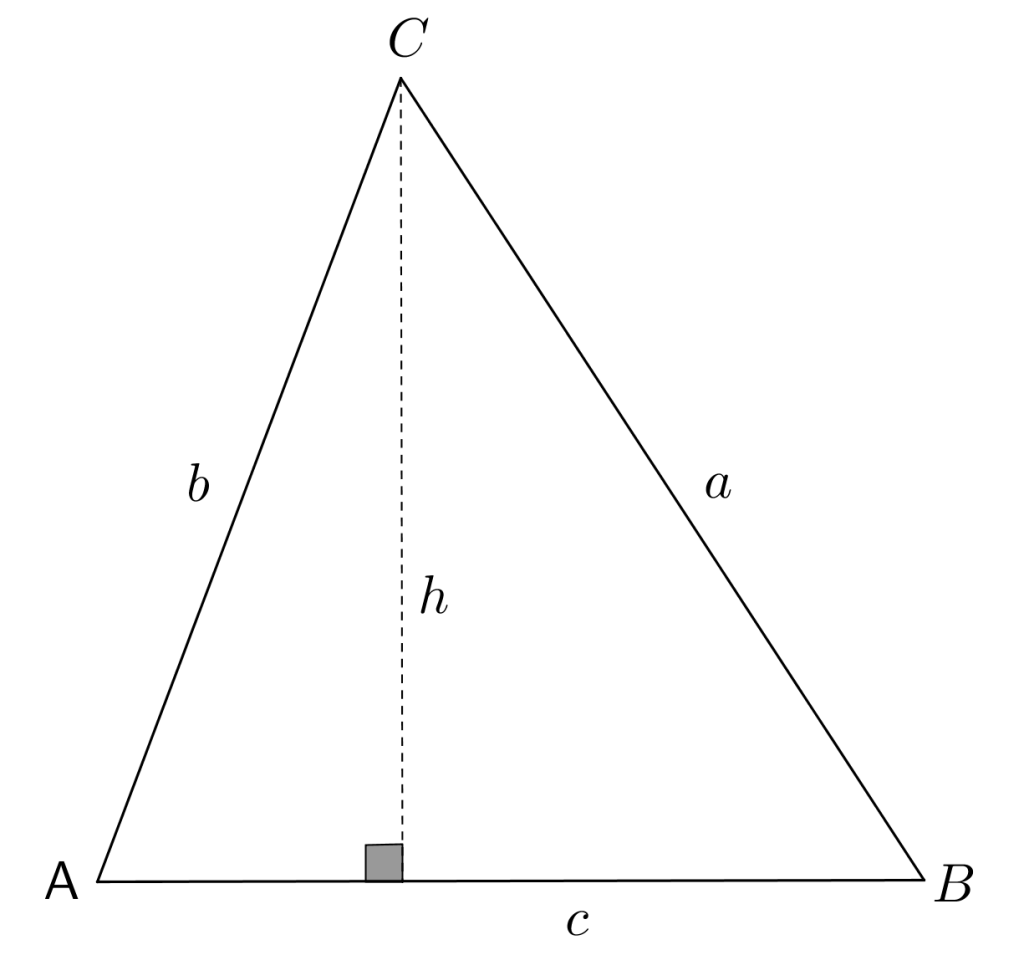
A área do triângulo em questão é [tex]1[/tex], logo
[tex]\qquad\qquad \dfrac{hc}{2}=1. \qquad\qquad(i)[/tex]
Mas se [tex]\hat{A}[/tex] denota o ângulo definido pelo vértice [tex]A[/tex], então
[tex]\qquad\qquad sen\hat{A}=\dfrac{h}{b}. \qquad\qquad(ii)[/tex]
De [tex](i)[/tex] e [tex](ii)[/tex] segue, então, que
[tex]\qquad\qquad \dfrac{bc}{2}sen\hat{A}=1. \qquad\qquad(iii)[/tex]
Mas o seno de um ângulo é limitado superiormente por [tex]1[/tex], logo, em particular, [tex]sen{\hat{A}}\le 1[/tex] e, já que [tex]\dfrac{bc}{2}\gt 0[/tex], podemos concluir que
[tex]\qquad\qquad \dfrac{bc}{2}sen{\hat{A}}\leq \dfrac{bc}{2}. \qquad\qquad(iv)[/tex]
De [tex](iii)[/tex] e [tex](iv)[/tex] temos que
[tex]\qquad\qquad 1=\dfrac{bc}{2}sen\hat{A}\leq \dfrac{bc}{2}[/tex]
e, assim,
[tex]\qquad\qquad 1\leq \dfrac{bc}{2}. \qquad\qquad(v)[/tex]
Como [tex]b \geq c[/tex], então [tex]\dfrac{b^2}{2} \geq \dfrac{bc}{2}[/tex] e, portanto, de [tex](v)[/tex], segue que [tex]\dfrac{b^2}{2} \geq 1[/tex].
Assim [tex]b^2\geq 2[/tex] e, sendo [tex]b > 0[/tex], concluímos, finalmente, que [tex]\boxed{ b \geq \sqrt{2}}[/tex].
Nada garante as alternativas [tex](a),(c),(d)[/tex].
Observação: Perceba que, embora a figura mostre um triângulo cujo ângulo [tex]\hat{A}[/tex] é agudo, a igualdade [tex](iii)[/tex] ainda é válida nos casos em que [tex]\hat{A}[/tex] é um ângulo reto, ou mesmo obtuso. Portanto a figura ilustrativa não tira a generalidade da solução.
Solução elaborada pelos Moderadores do Blog.
Nível C – Questão Difícil
