Problema
Um terreno quadrado foi dividido em cinco partes retangulares iguais.
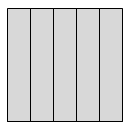
Se o perímetro de cada parte retangular resultante da divisão é 150 metros, qual é o perímetro do terreno quadrado?
Solução
Suponha que [tex]a[/tex] seja a largura, em metros, de cada um dos terrenos retangulares resultantes da divisão.
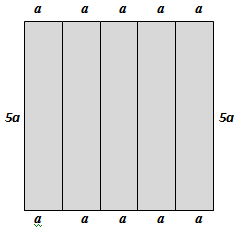
Como o perímetro de cada parte retangular é 150 metros, então
[tex]\quad 5a+a+5a+a=150\\
\quad 12a=150\\
\quad a=\dfrac{150}{12}=\dfrac{25}{2}[/tex].
Dessa forma, o perímetro do terreno quadrado é
[tex]\quad 4\cdot(5a)=4\cdot (5 \cdot\dfrac{25}{2})=250[/tex]
e, portanto, o perímetro do terreno quadrado é 250 metros.
Solução elaborada pelos Moderadores do Blog.
Segunda Gincana de 2015 – Clubes de Matemática da OBMEP
Nível C – Questão Fácil
Nível C – Questão Fácil
