Problema
(Indicado a partir do 1º ano do E. M.)
Um curso de idiomas oferta as línguas Alemão, Inglês, Francês e Russo e possui [tex]150[/tex] alunos. Sabe-se que ninguém estuda simultaneamente Francês e Russo. Sabe-se ainda que dentre todos os alunos
– [tex]22[/tex] estudam apenas Alemão;
– [tex]20[/tex] estudam apenas Inglês;
– [tex]20[/tex] estudam apenas Francês;
– [tex]20[/tex] estudam apenas Alemão e Russo;
– [tex]6[/tex] estudam apenas Francês e Inglês;
– [tex]4[/tex] estudam apenas Alemão e Francês;
– [tex]24[/tex] estudam Russo e Inglês;
– [tex]28[/tex] estudam apenas Russo;
– [tex]1[/tex] estuda apenas Alemão e Inglês.
Quantas pessoas estudam simultaneamente Alemão, Francês e Inglês?
Solução
Observe a distribuição no diagrama de Venn das informações dadas no texto-base, onde x é o número de pessoas que estudam simultaneamente Francês, Inglês e Alemão.
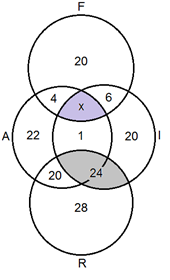
Como o total de pessoas é [tex]150[/tex], podemos encontrar x por meio da equação
[tex]\qquad\qquad20+4+x+6+22+1+20+20+24+28=150[/tex].
Assim, [tex]x=5[/tex], isto é, e o número de alunos que estudam simultaneamente as línguas Alemão, Francês e Inglês é [tex]5[/tex].
Solução elaborada pelos Moderadores do Blog.
