Problema
(Indicado a partir do 8º ano do E. F.)
O xadrez é um jogo que utiliza um tabuleiro quadriculado do tipo 8 x 8 e algumas peças.
- Uma das peças nesse jogo é o cavalo, que é a única peça que pode pular outras. O cavalo tem um movimento especial que parece a letra L: avançando duas casas na horizontal ou vertical e uma casa na direção perpendicular a primeira direção adotada.
Se um cavalo encontra-se numa das casas situadas num dos vértices do tabuleiro de xadrez, é possível esse cavalo chegar à casa diagonalmente oposta, realizando os seus movimentos previstos no jogo e visitando todas as outras casas exatamente uma vez ao longo do caminho?
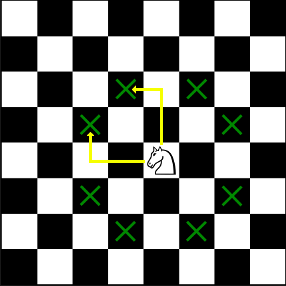
Solução 1
Suponha, sem perda de generalidade, que o cavalo parta de uma casa preta.
Quando o cavalo faz uma quantidade ímpar de movimentos, ele para numa casa branca e, quando a quantidade de movimentos é par, o cavalo termina seu trajeto numa casa preta. Até chegar na última casa, ele deve fazer 63 movimentos a fim de visitar todas as casas do tabuleiro um única vez (o tabuleiro tem 64 casas e ele já começa na casa do canto). Mas se ele fizer 63 movimentos, ele vai parar numa casa branca, o que impossibilita realizar a tarefa proposta, pois ele teria que terminar numa preta.
A ideia é análoga para o caso em que ele começa numa casa branca. Portanto, realizar tal percurso é impossível!
Solução elaborada pelo COM Os Nóbregas, com contribuições dos Moderadores do Blog.
Solução 2
Perceba que o quadrado inicial e final de um suposto trajeto possuem mesma cor. Em cada movimento, um cavalo salta de um quadrado de uma cor para um quadrado de cor oposta.
Para realizar a façanha sugerida, o cavalo deveria realizar 63 movimentos e, após estes, chegaria a um quadrado de cor oposta a inicial.
Logo, não é possível realizar um percurso como o questionado.
Solução elaborada pelos Moderadores do Blog.
Participou da discussão o Clube: Os Nóbregas.
