.Problemão: Esferas em contato

Problema
(Indicado a partir do 3º ano do E. M.)

Existe uma esfera que seja tangente às quatro esferas dadas, simultaneamente?
Em caso afirmativo, determine seu raio e, em caso negativo, justifique sua resposta.

Solução

• uma esfera interior às quatro esferas dadas
• outra esfera exterior às quatro esferas dadas,

como ilustra a figura abaixo.

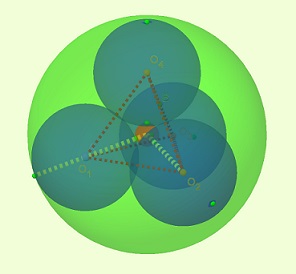
Na representação geométrica abaixo, procuramos ilustrar a vista do plano que passa pelo centro [tex]O[/tex] da “quinta” esfera (interna ou externa, tanto faz, pois é o mesmo) e pelos pontos [tex]O_1[/tex] e [tex]O_2[/tex], centros de duas das esferas dadas.
Assim, temos o triângulo [tex]O_1O_2B[/tex], onde [tex]B[/tex] é o ponto médio da aresta reversa de [tex]O_1O_2[/tex], no tetraedro cujos vértices são os centros [tex]O_1[/tex],[tex]O_2[/tex],[tex]O_3[/tex],[tex]O_4[/tex] das esferas dadas.

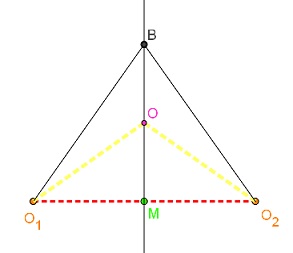
Pela simetria do tetraedro, podemos concluir que [tex]O[/tex] é o ponto médio de [tex]MB[/tex] (sendo [tex]M[/tex] o ponto médio de [tex]O_1O_2[/tex]).
Note que [tex]O_1B=O_2B[/tex] são apótemas do tetraedro de aresta [tex]2R[/tex] e, portanto, suas medidas são [tex]R\sqrt{3}[/tex].
Sendo assim, por Pitágoras, no triângulo [tex]O_1BM[/tex], podemos concluir que [tex]BM=R\sqrt{2}[/tex] e, consequentemente, [tex]OM=\frac{R\sqrt{2}}{2}[/tex].
Novamente, por Pitágoras (agora no triângulo[tex]O_1OM[/tex]), temos que [tex]O_1O=\dfrac{R\sqrt6}{2}[/tex].
Assim, os raios procurados podem ser obtidos, respectivamente, pela diferença (para a esfera interna) e soma (para a esfera externa) desta medida com o raio das esferas inicialmente dadas.
Finalmente, para a esfera interior, temos que o seu raio [tex]R_1[/tex] pode ser obtido por:
[tex]\qquad R_1=R\left(\dfrac{\sqrt6}2-1\right)[/tex]
e para a esfera exterior, temos que o seu raio [tex]R_2[/tex] pode ser obtido por:
[tex]\qquad R_2=R\left(\dfrac{\sqrt6}2+1\right).[/tex]

Solução elaborada pelos Moderadores do Blog.

Testando a solução

Bons estudos!