Um pouco sobre divisibilidade – Critérios de divisibilidade, sem justificativas

Critérios de divisibilidade

Nesta Sala, apresentaremos alguns dos tradicionais critérios de divisibilidade.
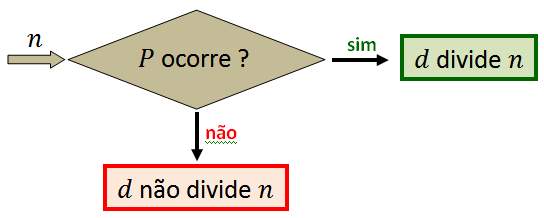
Fixado um número natural não nulo [tex]d[/tex], um critério de divisibilidade é uma condição [tex]P[/tex] necessária e suficiente para que um número natural seja divisível por [tex]d[/tex], portanto algo do tipo:

Um número natural n é divisível por d se, e somente se P.

Isso não só significa que significa que “se [tex]P[/tex] ocorre, então n é divisível por [tex]d[/tex]”, mas também significa que “se a condição [tex]P[/tex] não ocorre, então [tex]n[/tex] não é divisível por [tex]d[/tex]”.

criterio

Divisibilidade por 2

Um número natural [tex]n[/tex] é divisível por [tex]2[/tex] se, e somente se, terminar em [tex]0[/tex], ou [tex]2[/tex], ou [tex]4[/tex], ou [tex]6[/tex], ou [tex]8[/tex].

  • 15638748 é divisível por 2, pois termina em 8.
  • 6749029876539871375986 é divisível por 2, pois termina em 6.
  • 7629817 não é divisível por 2, pois termina em 7.
  • 2578014971 não é divisível por 2, pois termina em 1.

Divisibilidade por 3

Um número natural [tex]n[/tex] é divisível por [tex]3[/tex] se, e somente se, a soma de seus algarismos for divisível por [tex]3[/tex].

  • 3741 é divisível por 3, pois 3+7+4+1=15 e 15 é divisível por 3.
  • 100104053 não é divisível por 3, pois 1+0+0+1+0+4+0+5+3=14 e 14 não é divisível por 3.
  • 80200010103 é divisível por 3, pois 8+0+2+0+0+0+1+0+1+0+3=15 e 15 é divisível por 3.
  • 738295698 também é divisível por 3. Observe que
    7+3+8+2+9+5+6+9+8=57     e    5+7=12.
    Como 12 é divisível por 3, 57 é divisível por 3, portanto 738295698 também o é.
  • 19274654327498765128376538476253849631 também é divisível por 3. Observe que
    1+9+2+7+4+6+5+4+3+2+7+4+9+8+7+6+5+1+2+8+3+7+6+5+3+8+4+7
    +6+2+5+3+8+4+9+6+3+1=190    e    1+9+0=10.
    Como 10 não é divisível por 3, 190 não é divisível por 3, portanto 19274654327498765128376538476253849631 também não é.

Divisibilidade por 4

Um número natural [tex]n[/tex], com mais de dois algarismos, é divisível por [tex]4[/tex] se, e somente se, o número formado por seus dois últimos algarismos for divisível por [tex]4[/tex].

  • 1289824 é divisível por 4, pois 24 é divisível por 4.
  • 78961287453616 é divisível por 4, pois 16 é divisível por 4.
  • 248768564518 não é divisível por 4, pois 18 não é divisível por 4.
  • 7512398756902405975012587434 não é divisível por 4, pois 34 não é divisível por 4.

Divisibilidade por 5

Um número natural [tex]n[/tex] é divisível por [tex]5[/tex] se, e somente se, terminar em [tex]0[/tex], ou [tex]5[/tex].

  • 2346560 é divisível por 5, pois termina em 0.
  • 98387468597839789354905698115 é divisível por 5, pois termina em 5.
  • 889977556699881234 não é divisível por 5, pois termina em 4.
  • 18635987356259875410397602397423029737 não é divisível por 5, pois termina em 7.

Divisibilidade por 6

Um número natural [tex]n[/tex] é divisível por [tex]6[/tex] se, e somente se, [tex]n[/tex] for divisível, simultaneamente, por [tex]2[/tex] e [tex]3[/tex].

  • 618024 é divisível por 6, pois
    618024 é divisível por 2 (termina em 4);
    618024 é divisível por 3 (6+1+8+0+2+4=21 que é divisível por 3).
  • 87400012 não é divisível por 6, pois, embora seja divisível por 2 (termina em 2), 87400012 não é divisível por 3 (8+7+4+0+0+0+1+2=22 e 22 não é divisível por 3).
  • 2451093 não é divisível por 6, pois, embora seja divisível por 3 (2+4+5+1+0+9+3=24 e 24 é divisível por 3), 2451093 não divisível por 2 (termina em 3).

Divisibilidade por 7

Um número natural n é divisível por [tex]7[/tex] se, e somente se, a diferença entre o número obtido de n retirando-se o algarismo das unidades e o dobro do algarismo das unidades, tomada positivamente, for divisível por [tex]7[/tex].

(O positivamente aqui significa que devemos fazer a diferença entre o maior e o menor dos números obtidos.)

Se o número obtido ainda for grande, repete-se o processo, tantas vezes quanto for necessário, até que se possa verificar se o número final obtido é ou não divisível por [tex]7[/tex].

  • [tex]2799588[/tex] não é divisível por [tex]7[/tex]. Observe:
  • [tex]279958-2\cdot 8=279958-16=279942[/tex]
  • [tex]27994-2\cdot 2=27994-4=27990[/tex]
  • [tex]2799-2\cdot 0=2799[/tex]
  • [tex]279-2\cdot 9=279-18=261[/tex]
  • [tex]26-2\cdot1=26-2=24[/tex] e [tex]24[/tex] não é divisível por [tex]7[/tex]
    • [tex]5670[/tex] é divisível por [tex]7[/tex]. Observe:
  • [tex]567-2\cdot 0=567[/tex]
  • [tex]56-2\cdot 7=56-14=42[/tex] e [tex]42[/tex] é divisível por [tex]7[/tex]
    • [tex]100765[/tex] é divisível por [tex]7[/tex]. Observe:
  • [tex]10076-2\cdot 5=10076-10=10066[/tex]
  • [tex]1006-2\cdot 6=1006-12=994[/tex]
  • [tex]99-2\cdot 4=99-8=91[/tex]
  • [tex]9-2\cdot 1=9-2=7[/tex] e [tex]7[/tex] é divisível por [tex]7[/tex]

    • Divisibilidade por 8

    Um número natural [tex]n[/tex], com mais de três algarismos, é divisível por [tex]8[/tex] se, e somente se, o número formado por seus três últimos algarismos for divisível por [tex]8[/tex].

    • 2088 é divisível por 8, pois 088=88 é divisível por 8.
    • 47680114 não é divisível por 8, pois 114 não é divisível por 8.
    • 892398745632156789664 é divisível por 8, pois 664 é divisível por 8.
    • 859356874523698230002116 não é divisível por 8, pois 116 não é divisível por 8.

    Divisibilidade por 9

    Um número natural [tex]n[/tex] é divisível por [tex]9[/tex] se, e somente se, a soma de seus algarismos for divisível por [tex]9[/tex].

    • 5607801 é divisível por 9, pois 5+6+0+7+8+0+1=27 e 27 é divisível por 9.
    • 310579 não é divisível por 9, pois 3+1+0+5+7+9=25 e 25 não é divisível por 9.
    • 80200010103 não é divisível por 9, pois 8+0+2+0+0+0+1+0+1+0+3=15 e 15 não é divisível por 9 (embora 15 seja divisível por 3 e, consequentemente, o número 80200010103 seja divisível por 3).
    • 347382956988716576985 é divisível por 9. Observe que
      3+4+7+3+8+2+9+5+6+9+8+8+7+1+6+5+7+6+9+8+5=126    e    1+2+6=9.
      Como 9 é divisível por 9, 126 é divisível por 9, portanto 347382956988716576985 também o é.
    • 29174654327498765128376538476253849637 não é divisível por 9. Observe que
      2+9+1+7+4+6+5+4+3+2+7+4+9+8+7+6+5+1+2+8+3+7+6+5+3+8+4+
      +7+6+2+5+3+8+4+9+6+3+7=196    e    1+9+6=16.
      Como 16 não é divisível por 9, 196 não é divisível por 9; portanto 29174654327498765128376538476253849637 também não é divisível por 9.

    Divisibilidade por 10

    Um número natural [tex]n[/tex] é divisível por [tex]10[/tex] se, e somente se, terminar em [tex]0[/tex].

    • 47128520470 é divisível por 10, pois termina em 0.
    • 2587460123698520369750687268469793613678 não é divisível por 10, pois termina em 8.

    Divisibilidade por 11

    Um número natural [tex]n[/tex] é divisível por [tex]11[/tex] se, e somente se, a diferença entre a soma dos algarismos de ordem ímpar e a soma dos algarismos de ordem par, tomada positivamente, for um número divisível por [tex]11[/tex].
    As ordens ímpares e pares devem ser tomadas da direita para esquerda.

    O positivamente aqui significa que devemos fazer a diferença entre a maior e a menor somas.

    • 60367593 é divisível por 11; observe que:

      [tex]\begin{cases}
      S_i=3+5+6+0=14\\
      \\
      S_p=9+7+3+6=25
      \end{cases}\;\Longrightarrow \quad S_p-S_i=25-14=11[/tex]

      e [tex]11[/tex] é divisível por [tex]11[/tex].

    • 6268110 não é divisível por 11; observe que:

      [tex]\begin{cases}
      S_i=0+1+6+6=13\\
      \\
      S_p=1+8+2=11
      \end{cases}\;\Longrightarrow \quad S_i-S_p=13-11=2[/tex]

      e [tex]2[/tex] não é divisível por [tex]11[/tex].

    Divisibilidade por 12

    Um número natural [tex]n[/tex] é divisível por [tex]12[/tex] se, e somente se, [tex]n[/tex] for divisível, simultaneamente, por [tex]3[/tex] e [tex]4[/tex].

    • 236018024 é divisível por 12, pois
      236018016 é divisível por 4 (16 é divisível por 4);
      236018016 é divisível por 3 (2+3+6+0+1+8+0+1+6=27, que é divisível por 3).
    • 2350894312 não é divisível por 12, pois, embora seja divisível por 4 (12 é divisível por 4), 2350894312 não é divisível por 3 (2+3+5+0+8+9+4+3+1+2=37 e 37 não é divisível por 3).
    • 2451093 não é divisível por 12, pois, embora seja divisível por 3 (2+4+5+1+0+9+3=24 e 24 é divisível por 3), 2451093 não divisível por 4 (93 é divisível por 4).

    Divisibilidade por 13

    Um número natural n é divisível por [tex]13[/tex] se, e somente se, a soma entre o número obtido de n retirando-se o algarismo das unidades e o quádruplo do algarismo das unidades for divisível por [tex]13[/tex].
    Se o número obtido ainda for grande, repete-se o processo, tantas vezes quanto for necessário, até que se possa verificar se o número final obtido é ou não divisível por [tex]13[/tex].

    • [tex]16562[/tex] é divisível por [tex]13[/tex]. Observe:
  • [tex]1656+4\cdot 2=1656+8=1664[/tex]
  • [tex]166+4\cdot 4=166+16=182[/tex]
  • [tex]18+4\cdot 2=18+8=26[/tex] e [tex]26[/tex] é divisível por [tex]13[/tex]
    • [tex]33427[/tex] não é divisível por [tex]13[/tex]. Observe:
  • [tex]3342+4\cdot 7=3342+28=3370[/tex]
  • [tex]337+4\cdot 0=337[/tex]
  • [tex]33+4\cdot 7=33+28=61[/tex]
  • [tex]6+4\cdot 1=6+4=10[/tex] e [tex]10[/tex] não é divisível por [tex]13[/tex]

    • Divisibilidade por 14

    Um número natural [tex]n[/tex] é divisível por [tex]14[/tex] se, e somente se, [tex]n[/tex] for divisível, simultaneamente, por [tex]2[/tex] e [tex]7[/tex].

    • 7000 é divisível por 14, pois
      7000 é divisível por 2 (7000 é par);
      7000 é divisível por 7.
    • Números ímpares não são divisíveis por 14, pois, particularmente, não são divisíveis por 2.

    Divisibilidade por 15

    Um número natural [tex]n[/tex] é divisível por [tex]15[/tex] se, e somente se, [tex]n[/tex] for divisível, simultaneamente, por [tex]3[/tex] e [tex]5[/tex].

    • 60123825 é divisível por 15, pois
      60123825 é divisível por 3 (6+0+1+2+3+8+2+5 =27 que é divisível por 3)
      60123825 é divisível por 5 (termina em 5).
    • 210381 não é divisível por 15, pois, embora seja divisível por 3 (2+1+0+3+8+1= 15 que é divisível por 3), 210381 não é divisível por 5 (termina em 1).
    • 811045 não é divisível por 15, pois, embora seja divisível por 5 (termina em 5), 891045 não divisível por 3 (8+1+1+0+4+5=19 que não é divisível por 3).

    Divisibilidade por 16

    Um número natural [tex]n[/tex], com mais de quatro algarismos, é divisível por [tex]16[/tex] se, e somente se, o número formado por seus quatro últimos algarismos for divisível por [tex]16[/tex].

    • 236510144 é divisível por 16, pois 0144=144 é divisível por 16.
    • 8923987456321567891325 não é divisível por 16, pois 1325 não é divisível por 16 (é ímpar).
    • 830298547963214520032 é divisível por 16, pois 0032=32 é divisível por 16.

    Um critério geral

    Sejam [tex]a[/tex] e [tex]b[/tex] números naturais tais que [tex]mdc(a,b)=1.[/tex]
    Um número natural [tex]n[/tex] é divisível por [tex]a\cdot b[/tex] se, e somente se, [tex]n[/tex] for divisível simultaneamente por [tex]\, a \,[/tex] e [tex]\, b.[/tex]

    • Um número natural [tex]n[/tex] é divisível por [tex]45[/tex] se, e somente se, [tex]n[/tex] for divisível simultaneamente por [tex]5[/tex] e [tex]9[/tex].
    • Um número natural [tex]n[/tex] é divisível por [tex]66[/tex] se, e somente se, [tex]n[/tex] for divisível simultaneamente por [tex]6[/tex] e [tex]11[/tex].
    • Um número natural [tex]n[/tex] é divisível por [tex]99[/tex] se, e somente se, [tex]n[/tex] for divisível simultaneamente por [tex]9[/tex] e [tex]11[/tex].

    Equipe COM – OBMEP

    Voltar para Sala Principal

    Link permanente para este artigo: http://clubes.obmep.org.br/blog/um-pouco-sobre-divisibilidade-criterios-de-divisibilidade-sem-justificativas/