Problema
(Indicado a partir do 9º ano do E. F.)
Como podemos colocar uma simples cerca em linha reta entre dois terrenos, mostrados na figura a seguir, de modo a substituir as duas cercas, em ângulo, mas mantendo a área original de cada terreno?
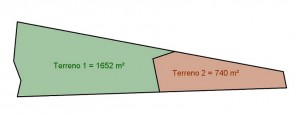
Vejam, a seguir, uma imagem ampliada da cerca a ser substituída.
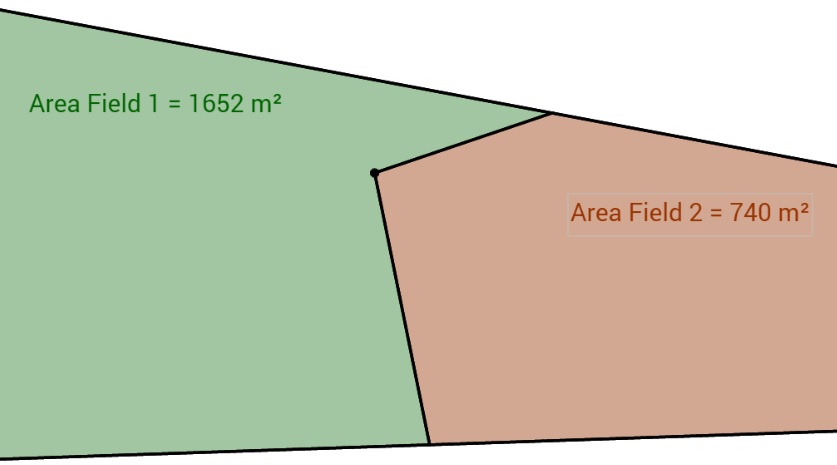
Solução
Sejam A, B e C os pontos como indicados na figura abaixo. A ideia, então, é traçarmos a reta AB e uma paralela a esta, passando por C, como ilustra a figura a seguir.
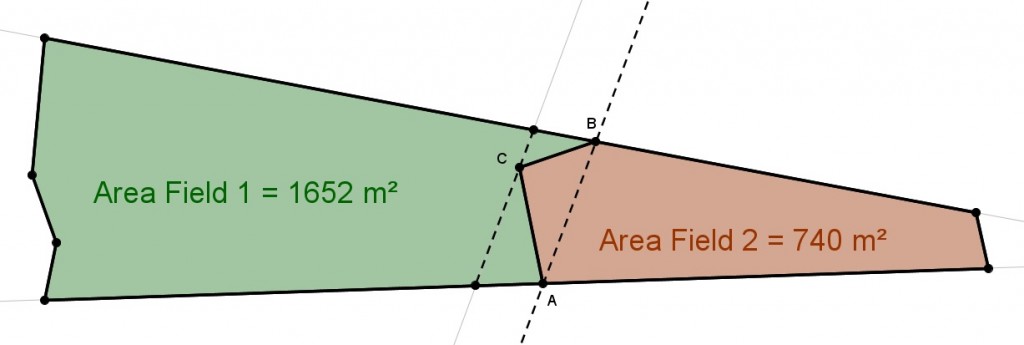
Dessa forma, movendo o ponto C sobre a reta construída como paralela à reta AB, teremos um triângulo sempre com área equivalente ao triângulo ABC original. Assim, preservamos a área da figura e ajustamos convenientemente, como o exemplo que se segue.
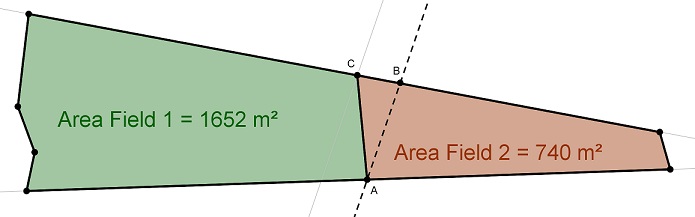
Solução elaborada pelos Moderadores do Blog.
Testando a solução
Você pode utilizar o applet abaixo para observar a veracidade da afirmação demonstrada para terrenos medindo [tex]1050[/tex] e [tex]630[/tex] unidades de área, quantas vezes você quiser!
Basta seguir as instruções e boa diversão!
1) Mova o ponto [tex]C[/tex] para obter as possíveis cercas que resolvem o problema.
2) Além das áreas dos dois terrenos, são exibidas as áreas dos três triângulos que ficam definidos pelas duas retas construídas e pelo ponto [tex]C[/tex].
Observem que, movimentando o ponto [tex]C[/tex]:
- as áreas dos dois terrenos não se modificam;
- as áreas definidas pelos triângulos [tex]T_1[/tex] e [tex]T_2[/tex] se modificam, mas a soma delas se mantém;
- a área definida pelo triângulo [tex]T_3[/tex] não se modifica.
3) Lembramos que o GeoGebra fornece valores aproximados para as medidas apresentadas.
4) Para voltar para a configuração inicial, é só clicar nas setinhas que aparecem no canto superior direito do applet.
OBMEP_ srdg, criado com o GeoGebra
