Problema
(Indicado a partir do 9º ano do E. F.)
No trapézio [tex]ABCD[/tex] com bases [tex]AB[/tex] e [tex]CD[/tex], temos as seguintes medidas:
- [tex]AB = 52[/tex],
- [tex]BC = 12[/tex],
- [tex]CD = 39[/tex]
- [tex]DA = 5[/tex].
Qual a área do trapézio [tex]ABCD[/tex]?
Solução
Prolongando [tex]\overline{AD}[/tex] e [tex]\overline{BC}[/tex] temos o ponto [tex]E[/tex] de intersecção, como na figura abaixo:
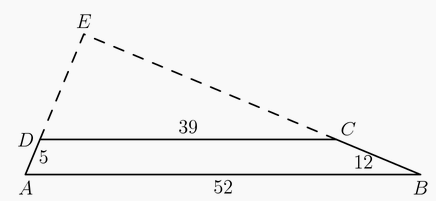
Como [tex]\overline{AB}[/tex] e [tex]\overline{CD}[/tex] são paralelos, temos uma semelhança entre [tex]\triangle AEB[/tex] e [tex]\triangle DEC[/tex], sendo a razão de proporcionalidade [tex]\frac {39}{52} = \frac {3}{4}[/tex].
Logo
[tex] \qquad \dfrac {CE}{CE + 12} = \dfrac {3}{4}[/tex], donde [tex]CE = 36[/tex],
[tex] \qquad \dfrac {DE}{DE + 5} = \dfrac {3}{4} [/tex], donde [tex] DE = 15[/tex].
Dessa forma, os lados do [tex]\triangle CDE[/tex] medem [tex]15, 36[/tex] e [tex]39[/tex], ou seja, o [tex]\triangle CDE[/tex] é um triângulo retângulo, já que:
[tex]\qquad \qquad 15^2+36^2=225+1296=1521=39^2[/tex].
Assim, o [tex]\triangle AEB[/tex] também é retângulo, e seus catetos medem [tex]15 + 5 = 20[/tex] e [tex]36+ 12 = 48[/tex].
Portanto, a área do trapézio, [tex]S(ABCD)[/tex], é obtida da seguinte forma:
[tex]S(ABCD) = S(ABE) – S(CDE) = \frac {1}{2} \cdot 20 \cdot 48 – \frac {1}{2} \cdot 15 \cdot 36 = 210[/tex] unidades de área.
Solução elaborada pelos Moderadores do Blog.
