Problema
(Indicado a partir do 1º ano do E. M.)
Um avião de 100 lugares foi fretado para uma excursão.
A companhia exigiu de cada passageiro R$ 800,00, mais R$ 10,00 por cada lugar vago.
Para que número de passageiros a receita da empresa será máxima?

Solução
Seja [tex]p[/tex] o número de passageiros da excursão, então o número de poltronas vagas é dado por [tex]100-p[/tex].
Assim, a expressão que fornece a receita em função de [tex]p[/tex] é dada por
[tex]\qquad \quad R(p)=(800+10(100-p))p=1800p-10p^2[/tex].
Como essa expressão representa o gráfico de uma função quadrática (parábola com a concavidade para baixo) cujas raízes são [tex]0[/tex] e [tex]180[/tex], então o valor de [tex]p[/tex] que resultará em uma receita máxima será [tex]90[/tex], devido à simetria da parábola.
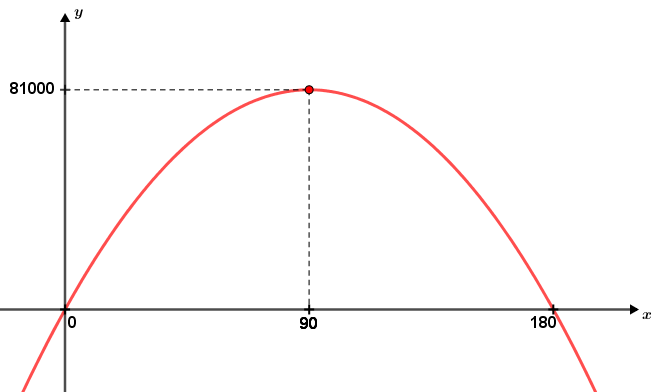
Assim, o número de passageiros que propiciará a receita máxima para a empresa será [tex] \,\fcolorbox{black}{#eee0e5}{$90$}\,[/tex] e, embora não solicitada no problema, essa receita será de [tex] \,\fcolorbox{black}{#eee0e5}{$R\$\,81\,000$}\,[/tex].
Solução elaborada pelos Moderadores do Blog.
