.Problema de Gincana: Duas funções e uma distância

Problema

Na figura temos esboçados os gráficos de uma função quadrática [tex]f[/tex] e de uma função logarítmica [tex]g[/tex], definidas por [tex]f(x) = x^2 + 2x + 1[/tex] e [tex]g(x) = log_2 x[/tex].

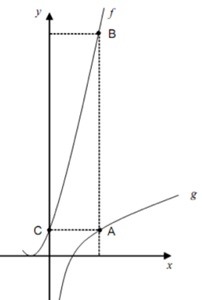
Sabendo que

[tex]C[/tex] é a interseção do gráfico da função [tex]f[/tex] com o eixo das ordenadas;
[tex]A[/tex] é o ponto do gráfico da função [tex]g[/tex] de mesma ordenada que [tex]C[/tex];
[tex]B[/tex] é o ponto do gráfico da função [tex]f[/tex] de mesma abscissa que [tex]A[/tex];

determine a distância entre os pontos [tex]A[/tex] e [tex]B[/tex].

Solução

Considere [tex]A = (x_A , y_A)[/tex], [tex]B = (x_B , y_B)[/tex] e [tex]C = (x_C , y_C)[/tex].
Inicialmente, observe que [tex]\boxed{ \, y_C = f(0) = 1}[/tex].
Além disso, [tex]g(x_A) = y_A[/tex] e [tex]\boxed{y_A = y_C = 1}[/tex]; portanto [tex]log_2 x_A = 1[/tex], donde [tex]\boxed{x_A =2^1= 2}[/tex].
Como [tex]f(x_B) = y_B[/tex], temos que [tex] \, x_B^2 + 2x_B + 1 = y_B \, [/tex]. Mas [tex]\boxed{x_B = x_A=2}[/tex], logo [tex] 2^2 + 2 \cdot 2 + 1 = y_B \, [/tex], donde [tex] \,\boxed{ y_B = 9}[/tex].
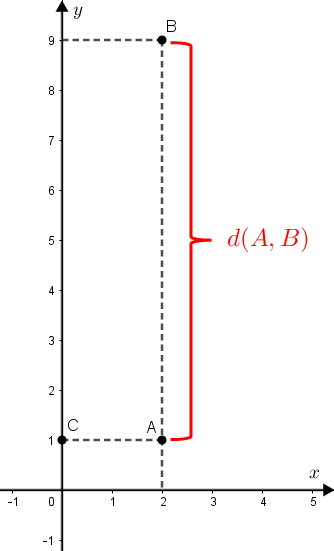
Como [tex]A\,[/tex] e [tex]\, B\,[/tex] têm a mesma abscissa, a distância entre [tex]A[/tex] e [tex]B[/tex], denotada por [tex]d(A , B)[/tex], finalmente pode ser calculada:
[tex]\qquad d(A , B)=y_B-y_A=9-1= \,\fcolorbox{black}{#eee0e5}{$8$}\,[/tex].