Problema
O lado AB do triângulo equilátero ABC é um diâmetro de uma circunferência de raio [tex]\frac{1}{2}[/tex].
Os pontos D e E são as interseções da circunferência com os lados BC e AC respectivamente.
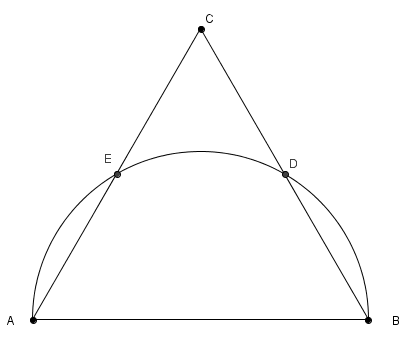
Neste caso, determine a distância de A até D.
Solução
Observe que o triângulo ABD está inscrito em um semicírculo, logo é um triângulo retângulo e, consequentemente, tem um ângulo reto.
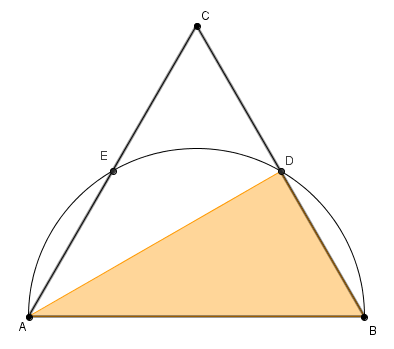
Observe, também, que:
- O ângulo cujo vértice é B não é o ângulo reto do triângulo ABD, já que este ângulo é também ângulo interno do triângulo equilátero ABC, medindo, portanto, 60°.
- O ângulo cujo vértice é A também não é o ângulo reto do triângulo ABD, já que a medida desse ângulo é menor do que a medida de um dos ângulos internos do triângulo equilátero ABC, medindo, portanto, menos do que 60°.
Dessa forma, o ângulo de vértice D é um ângulo reto e, portanto, o segmento AD é uma altura do triângulo equilátero ABC. Mas como o triângulo ABC é equilátero, AD é também uma mediana e, consequentemente, D é ponto médio do segmento BC.
Pelo exposto, temos que o segmento AD é um cateto de um triângulo retângulo cuja hipotenusa mede 1 e o segundo cateto mede [tex]\dfrac{1}{2}[/tex].
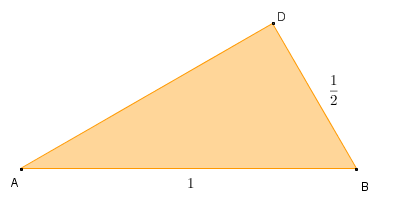
Dessa forma, se d é a distância entre os pontos A e D, então:
[tex]\qquad d=\sqrt{1-\dfrac{1}{4}}=\sqrt{\dfrac{3}{4}}=\dfrac{\sqrt{3}}{2}[/tex].
Logo, a distância entre os pontos A e D será de [tex]\dfrac{\sqrt{3}}{2}[/tex].
Solução elaborada pelos Moderadores do Blog.
Primeira Gincana de 2015 – Clubes de Matemática da OBMEP
Nível B – Questão Fácil
Nível B – Questão Fácil