Problema
(Indicado a partir do 8º ano do E. F.)
Nos lados [tex]\overline{AC}[/tex] e [tex]\overline{BC}[/tex] de um triângulo [tex]ABC[/tex] são tomados os pontos [tex]X[/tex] e [tex]Y[/tex], respectivamente, tais que [tex]A \hat{B}X \equiv Y \hat{A}C[/tex], [tex]A \hat{Y}B \equiv B \hat{X}C[/tex] e [tex]\overline{XC} \equiv \overline{YB}[/tex].
Determine as medidas dos ângulos internos do triângulo [tex]ABC[/tex].
Solução
Considere [tex]\alpha[/tex], [tex]\beta[/tex], [tex]\gamma[/tex], [tex]\delta[/tex] e [tex]\theta[/tex] as medidas em graus de [tex]C\hat{A}Y[/tex], [tex]A\hat{Y}B[/tex], [tex]Y\hat{A}B[/tex], [tex]A\hat{C}B[/tex] e [tex]X\hat{B}C[/tex] respectivamente.
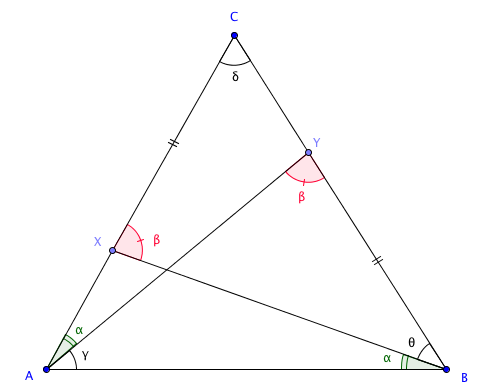
Temos [tex]\beta = 2 \alpha + \gamma \, [/tex] e [tex] \, \beta = \alpha + \delta \, [/tex], já que a medida de um ângulo externo de um triângulo é igual à soma das medidas dos ângulos internos não adjacentes a ele.
Assim, [tex] \, \delta = \alpha + \gamma \, [/tex] e, portanto, [tex] \, BC = AB \, [/tex], ou seja, o triângulo [tex] \, ABC \, [/tex] é isósceles.
Lema: Se dois triângulos possuem dois lados e um ângulo oposto a um deles ordenadamente congruentes, então os ângulos opostos ao outro lado em cada triângulo são congruentes ou suplementares.
Usando o lema para os triângulos [tex] \, CXB \, [/tex] e [tex] \, BYA \, [/tex], temos [tex] \, \theta = \gamma \, [/tex] ou [tex] \, \theta + \gamma = 180^{\circ} \, [/tex].
Entretanto, a segunda possibilidade não ocorre, pois
[tex]\qquad \theta + \gamma \lt (\alpha + \theta) + (\alpha + \gamma) \lt 180^{\circ}[/tex],
uma vez que somamos apenas dois ângulos internos do triângulo [tex]ABC[/tex].
Logo [tex] \, \theta = \gamma \, [/tex], donde [tex]\delta = \alpha + \gamma = \alpha + \theta[/tex].
Assim, o triângulo [tex]ABC[/tex] é equilátero e, portanto, possui os três ângulos internos medindo [tex]60^{\circ}[/tex].
Solução elaborada pelos Moderadores do Blog .
