Problema
(Indicado a partir do 8º ano do E. F.)
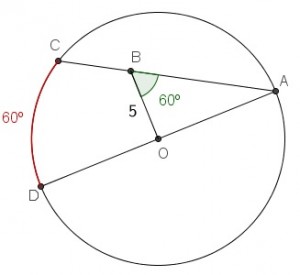
Na circunferência de centro [tex]O[/tex] da figura abaixo, o ponto [tex]B[/tex] está na corda [tex]AC[/tex], com [tex]OB=5[/tex].
Se o arco [tex]CD[/tex] e o ângulo [tex]O\hat{B}A[/tex] são ambos de [tex]60^\circ[/tex], determine o comprimento do segmento [tex]BC[/tex].
Solução
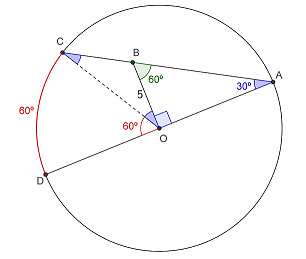
Observe, inicialmente, que [tex]C\hat{O}D=60^\circ[/tex] e [tex]C\hat{A}D=30^\circ[/tex] já que são, respectivamente, os ângulos central e inscrito que compreendem o arco [tex]CD[/tex], cuja medida é de [tex]60^\circ[/tex]. (Se necessário, veja a relação entre as medidas de um ângulo inscrito em uma circunferência e de seu respectivo ângulo central clicando aqui.)
Com isso, concluímos que [tex]A\hat{O}B=90^\circ[/tex], pela soma dos ângulos internos do triângulo [tex]AOB[/tex] e, consequentemente, [tex]B\hat{O}C=30^\circ[/tex]. (Se necessário, visite a Sala de Estudo sobre a soma dos ângulos internos de um triângulo clicando aqui.)
Como o ângulo [tex]O\hat{B}A[/tex] mede [tex]60^\circ[/tex], decorre que [tex]O\hat{C}B=30^\circ[/tex] e, portanto, o triângulo [tex]OBC[/tex] é isósceles.
Assim, o comprimento do segmento [tex]BC[/tex] é igual ao comprimento do segmento [tex]OB[/tex], ou seja, [tex] \,\fcolorbox{black}{#eee0e5}{$5$}\,[/tex].
Solução elaborada pelos Moderadores do Blog.
Participaram da discussão os Clubes: Bháskara Pitágoras; Fermatianos.
