Problema
(Indicado a partir do 9º ano do E. F.)
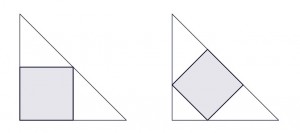
Há duas formas de “inscrever” um quadrado em um triângulo retângulo isósceles dado, como ilustram as figuras abaixo.
Se, no caso em que o quadrado tem maior área, sua área é 441 cm², qual é a área do quadrado no outro caso, considerando o mesmo triângulo retângulo dado?
Solução
Observe a figura abaixo. Note que, no primeiro caso, o quadrado representa [tex]\frac{1}{2}[/tex] da área do triângulo, enquanto que no segundo caso o quadrado representa [tex]\frac{4}{9}[/tex]. (Tente justificar essa afirmação.)
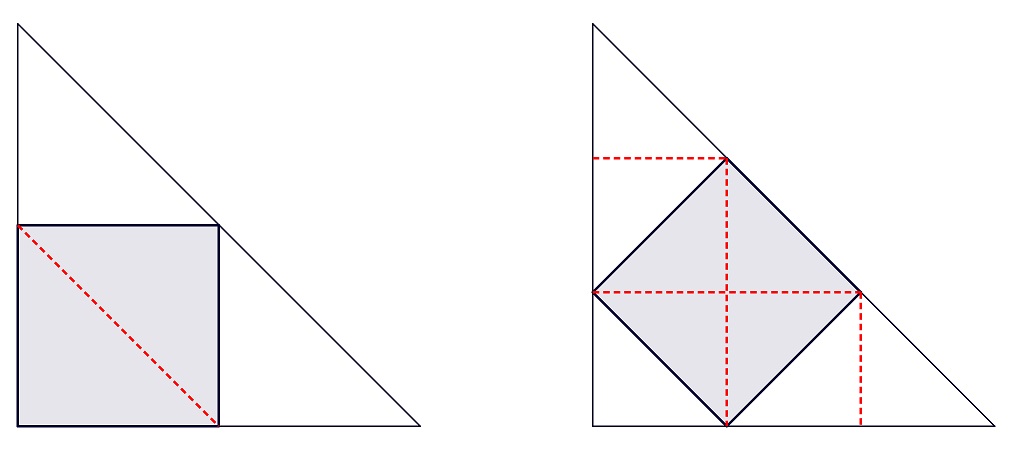
Como a área do quadrado maior é de 441 cm², então a área do triângulo é de 882 cm². Logo, a área do quadrado menor é dada por [tex]\frac{4}{9}[/tex] de 882 cm², ou seja, 392 cm².
Solução elaborada pelos Moderadores do Blog .
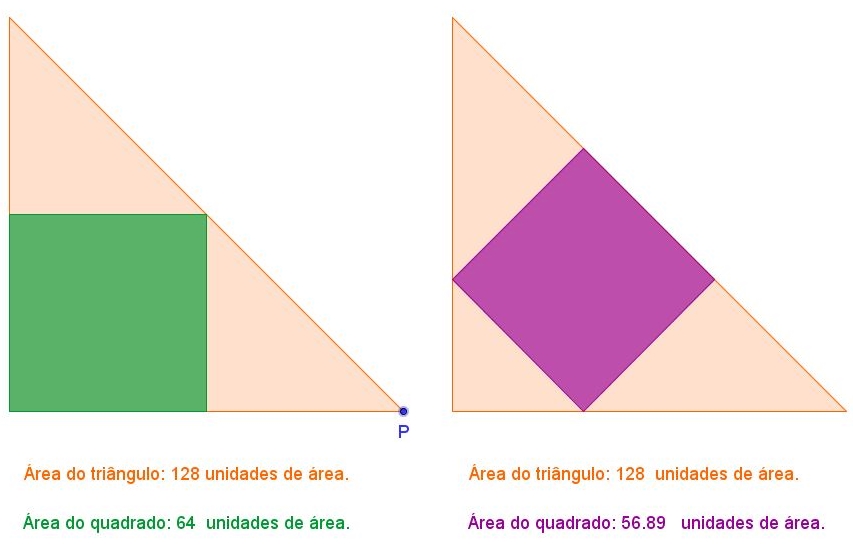
Um applet para ajudar
Você pode utilizar este applet para obter quadrados inscritos em vários triângulos retângulos isósceles e visualizar situações particulares da afirmação de que, nos dois casos considerados, a área do primeiro quadrado representa [tex] \bf{\frac{1}{2}}[/tex] da área do triângulo e, a do segundo quadrado, [tex]\bf{\frac{4}{9}}[/tex].
Duas observações importantes:
- O GeoGebra utiliza valores aproximados para representar números não inteiros.
- A visualização da propriedade não substitui a sua demonstração.
Clicando na imagem abaixo, o applet abrirá em uma outra janela – aí basta movimentar horizontalmente o ponto P para modificar, simultaneamente, os dois triângulos retângulos isósceles.