.Problema de Gincana: Um dado honesto e uma soma

Problema

Joga-se um dado duas vezes e, em cada lançamento, observa-se o número da face voltada para cima.
Qual a probabilidade de que a soma dos números obtidos seja [tex]7[/tex] ?

(a) [tex] \dfrac{1}{2}[/tex]
(b) [tex] \dfrac{1}{3}[/tex]
(c) [tex] \dfrac{1}{5}[/tex]
(d) [tex] \dfrac{1}{6}[/tex]
(e) Nenhuma das alternativas anteriores.

Solução

Duas observações iniciais:

O espaço amostral em questão tem [tex]36[/tex] elementos: no primeiro lançamento podemos obter seis faces e, consequentemente, seis números. Independentemente do número obtido, o dado é lançado novamente e, da mesma forma, podem aparecer seis números.
Considerando os dois números obtidos, a soma 7 poderá resultar de seis situações distintas:
[tex]\quad 1+6 \, ; \, 2+5 \, ; \, 3+4 \, ; \, 4+3 \, ; \, 5+2 \, ; \, 6+1[/tex].

Assim, são [tex]36[/tex] situações possíveis, das quais [tex]6[/tex] nos são favoráveis, o que nos dá uma probabilidade de [tex]\dfrac{6}{36}[/tex], ou seja, [tex]\dfrac{1}{6}[/tex].
Na tabela abaixo, podemos visualizar os pares que compõem o espaço amostral e, em destaque, os pares que fornecem as somas favoráveis.

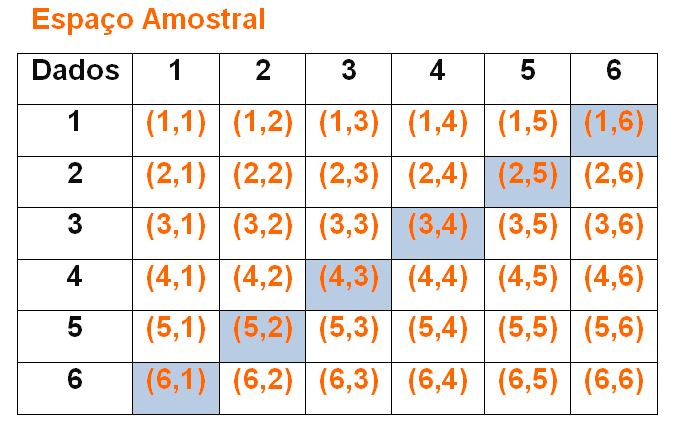
gincana