Problema
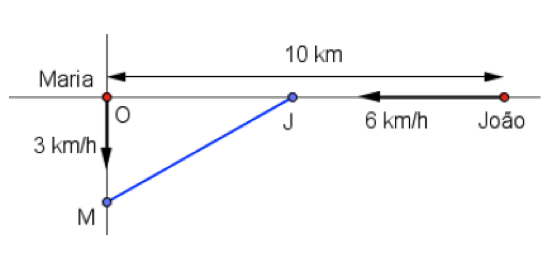
João mora a [tex]10[/tex] km a leste de Maria.
Num dia eles saem de casa ao mesmo tempo, andando em linha reta: João vai para o oeste a [tex]6[/tex] km/h e Maria para o sul a [tex]3[/tex] km/h. Determinar a menor distância possível entre eles.
(a) [tex]5 \,km[/tex].
(b) [tex]2\sqrt{5} \,km[/tex].
(c) [tex]4\sqrt{3}\, km [/tex].
(d) [tex]2\, km [/tex].
(e) [tex]\dfrac{4}{3}\, km[/tex].
Solução
Seja [tex]t[/tex] o tempo decorrido desde que João e Maria saíram de suas casas; indicaremos por [tex]d(t)[/tex] a distância entre eles no instante [tex]t[/tex].
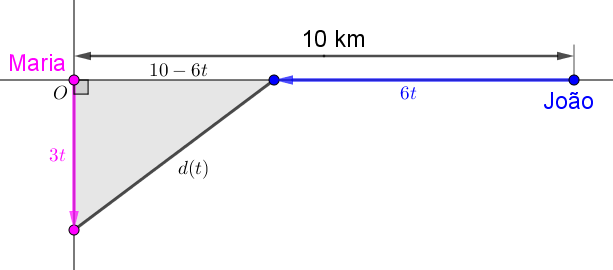
Utilizando o teorema de Pitágoras, temos
[tex]\qquad \qquad d(t) = \sqrt{(3t)^2 + (10-6t)^2}[/tex]
[tex]\qquad \qquad d(t) = \sqrt{45t^2-120t + 100}\,.[/tex]
A função [tex] \, d \, [/tex]é minimizada quando a função quadrática definida pelo radicando for mínima.
Assim, se [tex]f(t)=45t^2-120t + 100[/tex], o valor mínimo de [tex]d[/tex] é o valor mínimo de [tex]f[/tex], o que ocorre quando [tex]t = \dfrac{120}{90} = \dfrac{4}{3}[/tex].
Para esse valor de [tex] \, t[/tex] temos a distância mínima:
[tex]\qquad \qquad d_{min} = \sqrt{45 \left( \dfrac{4}{3}\right)^2-120 \cdot \frac{4}{3} + 100}[/tex]
[tex]\qquad \qquad d_{min} = \sqrt{45 \cdot \dfrac{16}{9}-120 \cdot \frac{4}{3} + 100}[/tex]
[tex]\qquad \qquad d_{min} = \sqrt{80-160 + 100}[/tex]
[tex]\qquad \qquad d_{min} = \sqrt{20} = 2 \sqrt{5}[/tex].
Assim, a distância procurada é de [tex] \, 2 \sqrt{5}\,km[/tex].
Observação: Poderíamos ter calculado o valor mínimo [tex]d_{min}[/tex] utilizando diretamente o valor mínimo de [tex]f[/tex], que denotaremos por [tex]f_{min}[/tex].
Acompanhe:
[tex]\qquad d_{min}=\sqrt{f_{min}}\\
\qquad d_{min}=\sqrt{\dfrac{4\cdot 45\cdot100-120^2}{4\cdot 45}}\\
\qquad d_{min}=\sqrt{\dfrac{18\,000-14\,100}{180}}\\
\qquad d_{min}=\sqrt{\dfrac{3600}{180}}\\
\qquad d_{min}=\sqrt{20}=2 \sqrt{5}.[/tex]
Solução elaborada pelos Moderadores do Blog.
Nível C – Questão Fácil

Ajuda, se precisar
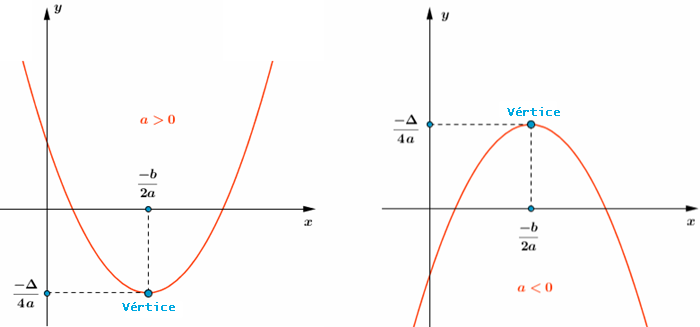
[tex]{\color{#800000}(1)}[/tex] O gráfico de uma função quadrática [tex]h:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]h(x)=ax^2+bx+c,a\not=0[/tex], é uma parábola com diretriz paralela ao eixo [tex]Ox[/tex], eixo de simetria paralelo ao eixo [tex]Oy[/tex], sendo sua concavidade voltada para cima se [tex]a\gt 0[/tex] e voltada para baixo se [tex]a\lt0[/tex].
[tex]{\color{#800000}(2)}[/tex] Se [tex]\Delta= b^2-4ac[/tex], as coordenadas do vértice da parábola são dadas por [tex](x_v,y_v)=\bigg(\dfrac{-b}{2a},\dfrac{-\Delta}{4a}\bigg)[/tex], sendo que [tex]x_v=\dfrac{-b}{2a} \, [/tex] e [tex] \, y_v=\dfrac{-\Delta}{4a}[/tex] indicam, respectivamente:
✓ o ponto de mínimo e o valor mínimo da função [tex]h[/tex], se a concavidade estiver voltada para cima;
✓ o ponto de máximo e o valor máximo da função [tex]h[/tex], se a concavidade estiver voltada para baixo.
Visualizem as informações fornecidas no lembrete [tex]{\color{#800000}(2)}[/tex], se [tex]\Delta \gt 0[/tex],
clicando no botão abaixo.