Problema
(Indicado a partir do 2º ano do E. M.)
Sobre uma superfície plana são dispostos palitos iguais formando figuras, como mostrado abaixo.
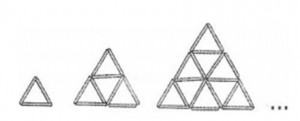
Contando os palitos de cada uma dessas figuras e denotando por an o número de palitos da n-ésima figura, encontra-se:
- a1 = 3,
- a2 = 9,
- a3 = 18, …
Determine, nesse caso, o valor de a100.
Solução
A sequência das figuras é:
- a1 = 3 palitos e 3 = 3 × 1
- a2 = 9 palitos e 9 = 3 + 6 = 3 + 3 × 2
- a3 = 18 palitos e 18 = 9 + 9 = 3 + 6 + 9 = 3 + 6 + 3 × 3
- a4 = 30 palitos e 30 = 18 + 12 = 9 + 9 + 12 = 3 + 6 + 9 + 12 = 3 + 6 + 9 + 3 × 4
- a5 = 45 palitos e 45 = 30 + 15 = 18 + 12 + 15 = 9 + 9 + 12 + 15 = 3 + 6 + 9 + 12 + 15 = 3 + 6 + 9 + 12 + 3 × 5
A primeira parcela da soma dos palitos para cada figura é sempre 3. Em cada soma, seguimos com os múltiplos de três até a última parcela, que será três vezes o número da figura correspondente. Assim para a figura 100 o número de palitos será:
a100 = 3 + 6 + 9 + 12 + 15 + 18 + … + 291 + 294 + 297 + 3 × 100 .
Também observamos que em cada soma a quantidade de parcelas corresponde ao número da figura, então em a100 somamos o primeiro com o último, o segundo com o penúltimo e assim por diante, obtendo sempre 303. Como temos 100 parcelas, serão 50 somas, então o número de palitos será:
a100 = 303 × 50 = 15150 .
Solução elaborada pelo Clube Todos pela Matemática, com contribuições dos Moderadores do Blog.
