Problema
(Indicado a partir do 9º ano do E. F.)
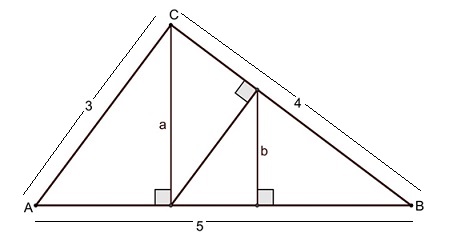
Na figura abaixo, o triângulo retângulo [tex]ABC[/tex] tem ângulo reto em [tex]C[/tex]. Além disso, sabe-se que [tex]AC=3[/tex], [tex]BC=4[/tex] e [tex]AB=5[/tex].
Nessas condições e considerando as indicações da figura, determine a razão [tex]\dfrac{a}{b}.[/tex]
Solução
Considere a figura abaixo.
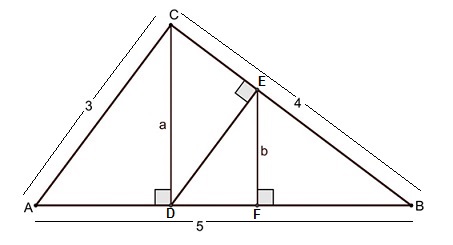
Observemos, inicialmente, que os triângulos [tex]\triangle ACB[/tex], [tex]\triangle ADC[/tex] e [tex]\triangle DEB[/tex] são todos semelhantes (convença-se disso).
Logo, por semelhança dos triângulos [tex]\triangle ADC[/tex] e [tex]\triangle ACB[/tex], temos que [tex]\dfrac{a}{3} = \dfrac{4}{5} [/tex], donde [tex] a = \dfrac{12}{5}.[/tex]
Além disso, observamos que, por semelhança dos triângulos [tex]\triangle ACB[/tex] e [tex]\triangle DEB[/tex]:
[tex]\qquad \dfrac{a}{b} = \dfrac{5}{DB}. \qquad \qquad \qquad (1)[/tex]
Note que, como
[tex]\qquad AD = \sqrt {3^2-\left(\dfrac{12}{5} \right)^2} = \dfrac{9}{5}[/tex],
então
[tex]\qquad DB = 5-AD = 5-\dfrac{9}{5} = \dfrac{16}{5}[/tex].
Finalmente temos, de [tex](1)[/tex], que:
[tex]\qquad\dfrac{a}{b} = \dfrac{5}{DB} = \dfrac{5}{1}\cdot \dfrac{5}{16}=\dfrac{25}{16}[/tex].
Solução elaborada pelos Moderadores do Blog.
