Problema
(Indicado a partir do 8º ano do E. F.)
Um certo relógio adianta-se regularmente.
Se a cada 61 minutos os ponteiros das horas e dos minutos se sobrepõem, quanto tempo o relógio adianta por hora?
Solução
Em um relógio convencional, o ponteiro das horas desloca-se [tex]30^\circ[/tex] por hora e, o dos minutos, [tex]360^\circ [/tex] por hora. Como ao meio-dia os dois ponteiros estão sobrepostos, então a próxima superposição dá-se após [tex]1 h+x[/tex] ([tex]x[/tex] em horas), onde [tex]x[/tex] é tal que [tex] 360x=30+30x[/tex].
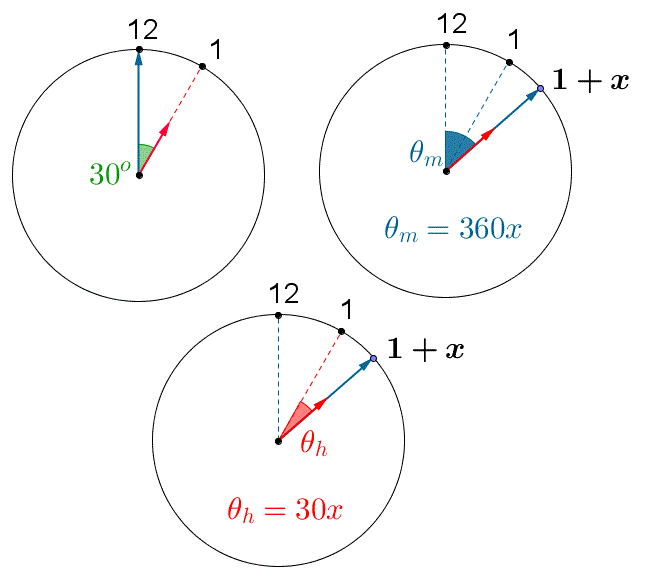
Assim, temos que:
[tex]\qquad 360x=30+30x\\
\qquad 360x=30(1+x)\\
\qquad 12x=1+x\\
\qquad 11x=1\\
\qquad x=\dfrac{1}{11}[/tex]
e, portanto, concluímos que
► em um relógio normal, os ponteiros encontram-se a cada [tex]\boxed{1+\dfrac{1}{11}=\dfrac{12}{11}~ horas} \;[/tex] ou [tex]\;\boxed{60+ \dfrac{60}{11}=\dfrac{720}{11}~minutos}[/tex].
Porém, sabemos que a cada [tex]61[/tex] minutos de um relógio convencional, os ponteiros daquele que adianta já estão sobrepostos; logo, após [tex]60[/tex] minutos do relógio convencional, o relógio que adianta indicará
[tex]\quad \quad \quad \dfrac{60 \times 720}{61 \times 11}=64+\dfrac{256}{61 \times 11},[/tex]
ou seja, um pouco mais de [tex]64[/tex] minutos e [tex]22[/tex] segundos.
Podemos, então, afirmar que o relógio impreciso adianta-se, aproximadamente, [tex]4[/tex] minutos e [tex]23[/tex] segundos por hora.
Solução elaborada pelos Moderadores do Blog.
