Problema
(Indicado a partir do 8º ano do E. F.)
Um filho matemático escreve ao pai, também matemático, pedindo dinheiro.
Desejando que o valor solicitado fosse expresso por meio de um código, o filho escreve a soma do número SEND com o número MORE cujo resultado é o número MONEY , valor solicitado por ele:

Na adição codificada, cada letra representa um único algarismo e um algarismo é representado por uma única letra; assim, quanto pediu o filho?
Solução
Observe, inicialmente, que na adição apresentada são utilizadas [tex]8 [/tex] letras diferentes, ou seja, [tex]8[/tex] algarismos diferentes, já que cada letra representa um único algarismo e cada algarismo só é representado por uma única letra.
Como a soma de dois algarismos distintos apresenta valor máximo [tex]17[/tex] ([tex]9+8=17[/tex]) e valor mínimo [tex]1[/tex] ([tex]0+1=1[/tex]), então, a partir da coluna das dezenas do esquema da adição apresentado, pode ser adicionado [tex]1[/tex] à soma dos algarismos de cada coluna (o famoso “vai 1”). Para ajudar, vamos colocar um “vai 1” nas colunas da segunda, terceira, quarta e quinta somas de algarismos (da direita para esquerda), como representamos a seguir. Durante a discussão do problema, verificaremos se o “vai 1” de cada coluna ocorre de fato ou não.
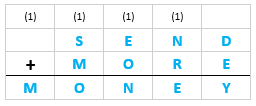
- MONEY é um número de cinco algarismos, logo podemos concluir que o quarto “vai 1” realmente ocorre e, portanto, [tex]\,\fcolorbox{black}{#CDE1F3}{$M=1$}\,[/tex].
Ficamos, a princípio, com o seguinte esquema da adição: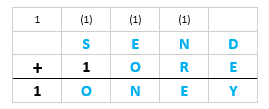
- Como [tex]S[/tex] é no máximo [tex]9[/tex], então a soma dos algarismos dos milhares apresenta valor [tex]11[/tex] ou [tex]10[/tex].
A ocorrência do valor [tex]11[/tex] implicaria [tex]O=1[/tex] ([tex]1\underline{1}=10+\underline{1}[/tex]) e neste caso teríamos [tex] M=O=1[/tex], o que não pode acontecer, já que letras distintas representam algarismos distintos. Portanto, a soma dos algarismos dos milhares é [tex]10[/tex], donde concluímos que [tex]\,\fcolorbox{black}{#CDE1F3}{$O=0$}\,[/tex] .
Podemos, então, reescrever o esquema da adição: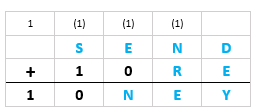
- Agora, observe a coluna das centenas no esquema anterior. Como devemos ter [tex]E \ne N[/tex], então aparece o “vai 1” na coluna das centenas, pois, do contrário, teríamos [tex]N=E+0=E[/tex].
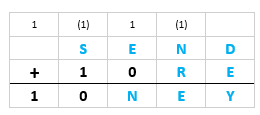
- Sendo a soma dos algarismos dos milhares igual a [tex]10[/tex], temos duas possibilidades:
[tex]\qquad 1+S+1=10[/tex] (ocorre o “vai 1” na coluna dos milhares) e, portanto, [tex]S=8[/tex]
ou
[tex]\qquad S+1=10[/tex] (não ocorre o “vai 1” na coluna dos milhares) e, portanto, [tex]S=9[/tex].
Analisemos essas duas possibilidades.Possibilidade 1
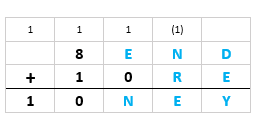
Esta possibilidade nos leva a um absurdo, já que, na coluna das centenas, [tex]1+ E + 0 \ge 10[/tex] , o que só é possível para [tex] E=9 [/tex] e, neste caso, teríamos [tex]N=O=0[/tex].
Então, é a Possibilidade 2 que ocorre.Possibilidade 2
Temos, então, necessariamente [tex]\,\fcolorbox{black}{#CDE1F3}{$S=9$}[/tex] e não aparece o “vai 1” na coluna dos milhares: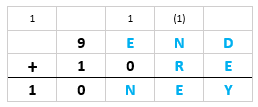
- Analisando as colunas das centenas e das dezenas do esquema da adição, concluímos que:
[tex]\qquad (i)\, N=E+1[/tex]
e
[tex]\qquad (ii)\, N + R=10 + E[/tex] ou [tex] N + R + 1 =10+E [/tex]
Analisemos as duas possibilidades da conclusão [tex](ii)[/tex]:
a) Se [tex] N+R=10+E [/tex], segue que:
[tex]\qquad (E+1)+R=10+E \\
\qquad R=9 [/tex]
e assim [tex] R=S=9[/tex], o que não pode ocorrer.
b) Temos, então, que [tex] N+R+1=10+E\,[/tex] e, portanto,
[tex]\qquad (E+1)+R+1=10+E\\
\qquad \,\fcolorbox{black}{#CDE1F3}{$R=8$}\, .[/tex]
Note que, neste caso, o “vai 1” na coluna das dezenas ocorre. Assim: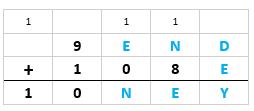
- Perceba que, da conclusão [tex](i)[/tex], temos que [tex]E\,[/tex] e [tex]\,N[/tex] são algarismos consecutivos, sendo [tex]N[/tex] o sucessor de [tex]E[/tex].
Resta descobrir os valores das letras [tex] E,\,N,\,D,\,Y[/tex] entre os algarismos [tex]2,\,3,\,4,\,5,\,6\,[/tex] e [tex]\,7[/tex]. Vamos lá!
- Observando a última configuração da adição, vemos que aparece um “vai 1” na coluna das dezenas; isso significa que [tex]D + E \ge 10[/tex]. Mas os algarismos [tex]0\,[/tex] e [tex]\,1[/tex] já foram utilizados; assim, de fato, [tex]D + E \ge 12[/tex].
Dentre os algarismos [tex]2,\,3,\,4,\,5,\,6,\,7[/tex], vemos que temos duas possibilidades para [tex]D\,[/tex] e [tex]\,E\,[/tex]: “[tex]7\,[/tex] e [tex]6[/tex]”, pois [tex]7+6=13[/tex], ou “[tex]7\,[/tex] e [tex]5[/tex]”, pois [tex]7+5=12[/tex].
Sabemos que [tex]N=E+1[/tex], o que nos permite concluir que [tex]E\ne7[/tex], pois, se [tex]E=7[/tex], teríamos que [tex]N=8[/tex], o que não poderia ocorrer pois já sabemos que [tex]R=8[/tex].
Assim “[tex]D=7\,[/tex] e [tex]\,E=5\,[/tex]” ou “[tex]D=7\,[/tex] e [tex]\,E=6[/tex]”. Perceba que com a segunda opção [tex]D[/tex] seria o sucessor de [tex]E[/tex], o que sabemos não ser verdade já que o sucessor de [tex]E[/tex] é [tex]N[/tex]. Dessa forma, [tex]\,\fcolorbox{black}{#CDE1F3}{$D=7$}\,[/tex] e [tex]\,\fcolorbox{black}{#CDE1F3}{$E=5$}\,[/tex].
E como [tex] N=E+1[/tex], obtemos também que [tex]\,\fcolorbox{black}{#CDE1F3}{$N=6$}\,[/tex].
Ufa, quase fechamos a adição. Veja!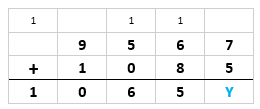
Para finalizar, somando os algarismos da coluna das unidades obtemos o valor de [tex]Y[/tex]: [tex]\fcolorbox{black}{#CDE1F3}{$Y=2$}\,[/tex], pois [tex]7+5=12=10+\underline{2}[/tex].
Portanto, completamos os termos da adição de modo único, conforme mostra a figura abaixo.
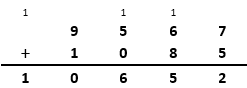
Pelo exposto, o valor solicitado pelo filho foi [tex] \,\fcolorbox{black}{#eee0e5}{$10\; 652$}\,[/tex].
Solução elaborada pelos Moderadores do Blog .
