Problema
(Indicado a partir do 1º ano do E. M.)
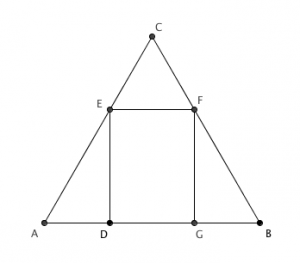
Na figura, [tex]ABC[/tex] é um triângulo equilátero de lado [tex]1[/tex] metro.
Qual a área máxima de um retângulo [tex]DEFG[/tex] tal que [tex]\overline{DG} ⊂ \overline{AB}[/tex], [tex]E ∈ \overline{AC}[/tex] e [tex]F ∈ \overline{BC}[/tex]?

Ajuda
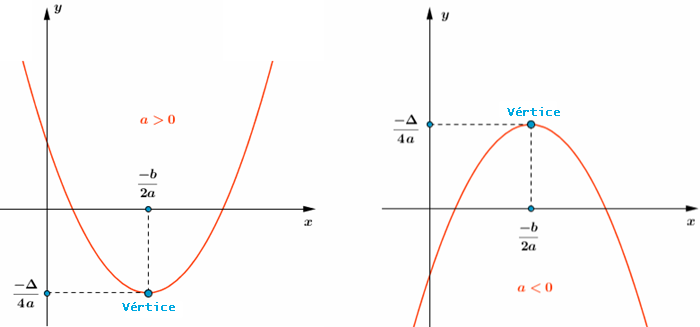
[tex]{\color{#800000}(1)}[/tex] O gráfico de uma função quadrática [tex]h:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]h(x)=ax^2+bx+c,\, a\not=0[/tex], é uma parábola com eixo de simetria paralelo ao eixo [tex]Oy[/tex], sendo sua concavidade voltada para cima se [tex]a\gt 0[/tex] e voltada para baixo se [tex]a\lt0[/tex].
[tex]{\color{#800000}(2)}[/tex] Se [tex]\Delta= b^2-4ac[/tex], as coordenadas do vértice da parábola são dadas por [tex](x_v,y_v)=\bigg(\dfrac{-b}{2a},\dfrac{-\Delta}{4a}\bigg)[/tex], sendo que [tex]x_v=\dfrac{-b}{2a}\, [/tex] e [tex]\, y_v=\dfrac{-\Delta}{4a}[/tex] indicam, respectivamente:
✓ o ponto de mínimo e o valor mínimo da função [tex]h[/tex], se a concavidade estiver voltada para cima;
✓ o ponto de máximo e o valor máximo da função [tex]h[/tex], se a concavidade estiver voltada para baixo.
Visualizem as informações fornecidas no lembrete [tex]{\color{#800000}(2)}[/tex], se [tex]\Delta \gt 0[/tex],
clicando no botão abaixo.
 |
Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex] Y[/tex], por [tex]\overline {XY} [/tex] e o seu comprimento por [tex]XY[/tex]. |
Solução
Seja [tex]\overline{CI}[/tex] a altura do [tex]\Delta ABC[/tex] relativa a [tex]\overline{AB}[/tex], conforme mostra a figura.
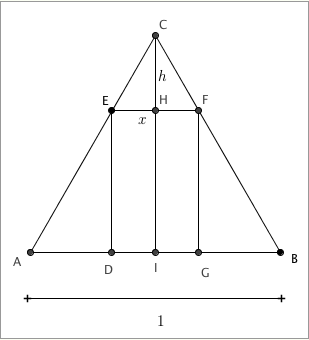
Num triângulo equilátero de lado [tex]1[/tex], todas as alturas são congruentes e medem [tex]\dfrac{\sqrt{3}}{2}[/tex]. (Verifique!)
Considere [tex]EF = x[/tex] e [tex]CH = h[/tex]. Da semelhança entre [tex]\Delta CEF[/tex] e [tex]\Delta CAB[/tex], segue que
[tex]\quad \quad \dfrac{x}{1} = \dfrac{h}{\dfrac{\sqrt{3}}{2}}\\
\quad \quad h = \dfrac{\sqrt{3}}{2}x\,.[/tex]
Podemos, então, escrever a área do retângulo [tex]DEFG[/tex] em função de [tex]x[/tex]:
[tex]\quad A(x) = \left( \dfrac{\sqrt{3}}{2}-h \right) \cdot x[/tex]
[tex]\quad A(x)=\left( \dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{3}}{2}x \right) \cdot x[/tex]
[tex]\quad \boxed{ A(x) =\dfrac{\sqrt{3}}{2}x-\dfrac{\sqrt{3}}{2}x^2}\,.[/tex]
Sendo essa área uma função quadrática de [tex]x[/tex], temos que seu valor máximo é dado por
[tex]\quad A_{M}=\dfrac{-\Delta}{4a}= \dfrac{-\left( \dfrac{\sqrt{3}}{2}\right)^2}{4\cdot \left(-\dfrac{\sqrt{3}}{2}\right)}\\
\quad A_{M} = \dfrac{-\dfrac{3}{4}}{-2\sqrt{3}}=\dfrac{3}{8\sqrt{3}} \\
\quad A_{M}= \dfrac{\sqrt{3}}{8}\,m^2\\
\quad A_{M}\approx 0,2165\,m^2\,.[/tex]
Você pode utilizar o aplicativo abaixo para observar um triângulo equilátero [tex]ABC[/tex] com lados medindo [tex]1\,m[/tex] e vários retângulos [tex]DEFG[/tex] definidos de acordo com as condições do problema. Com isso, você visualizará qual desses retângulos tem área máxima!
Um applet para ilustrar
No applet abaixo, movimente horizontalmente o ponto [tex]\textcolor{red}{D}[/tex] e observe que, para cada posição de [tex]\textcolor{red}{D}[/tex], você visualizará a área do retângulo [tex]\textcolor{red}{DEFG}[/tex] correspondente e o comprimento de seus lados.
Assim, você poderá visualizar que a área máxima que [tex]\textcolor{red}{DEFG}[/tex] pode ter é, aproximadamente, [tex]0,2165\,m^2\,.[/tex]
Instruções:
(1) Espere o applet carregar. (Ele pode demorar um pouquinho para carregar.)
(2) Para movimentar o ponto [tex]\textcolor{red}{D}[/tex] horizontalmente, clique sobre ele, mantenha o mouse pressionado e faça o movimento. (Se você estiver utilizando um celular ou um tablet, toque levemente no ponto [tex]\color{red}{D}[/tex] e movimente-o.)
OBMEP_ srdg, criado com o GeoGebra
Observamos que o applet ajuda na visualização do resultado;
mas, matematicamente, não substitui sua demonstração.
Solução elaborada pelos Moderadores do Blog .