.Problema: Comprimento de curva

Problema
(Indicado a partir do 8º ano do E. F.)

---

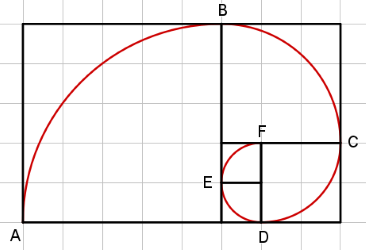
Calcule o comprimento [tex]C[/tex] da curva em vermelho abaixo, sabendo que os quadrados da malha quadriculada têm lado medindo [tex]1 \;\text{cm}[/tex] e cada um dos arcos inscritos nos quadrados possuem medida angular de [tex]90^{\circ}[/tex].

Solução

---

Como cada arco possui medida angular de [tex]90^{\circ}[/tex], então o comprimento de cada um deles é dado por [tex]\dfrac{1}{4}[/tex] do comprimento da circunferência cujo raio é a medida do lado do quadrado circunscrito ao respectivo arco. Dessa forma,

• o comprimento do arco [tex]\stackrel{\frown}{AB}[/tex] é [tex]\dfrac{1}{4}\cdot 2\cdot \pi \cdot 5 =\dfrac{1}{4}\cdot 10\pi[/tex];
• o comprimento do arco [tex]\stackrel{\frown}{BC}[/tex] é [tex]\dfrac{1}{4}\cdot 2\cdot \pi \cdot 3 =\dfrac{1}{4}\cdot 6\pi[/tex];
• o comprimento do arco [tex]\stackrel{\frown}{CD}[/tex] é [tex]\dfrac{1}{4}\cdot 2\cdot \pi\cdot 2 =\dfrac{1}{4}\cdot 4\pi[/tex];
• o comprimento do arco [tex]\stackrel{\frown}{DE}[/tex] é [tex]\dfrac{1}{4}\cdot 2\cdot \pi\cdot 1 =\dfrac{1}{4}\cdot 2\pi[/tex];
• o comprimento do arco [tex]\stackrel{\frown}{EF}[/tex] é [tex]\dfrac{1}{4}\cdot 2\cdot \pi\cdot 1 =\dfrac{1}{4}\cdot 2\pi[/tex].

Logo, o comprimento total da curva em vermelho é dado por

[tex]\qquad C = \dfrac{1}{4}\cdot 10\pi+\dfrac{1}{4}\cdot 6\pi+\dfrac{1}{4}\cdot 4\pi+\dfrac{1}{4}\cdot 2\pi+\dfrac{1}{4}\cdot 2\pi[/tex]
[tex]\qquad C = \dfrac{1}{4}(10\pi+6\pi+4\pi+2\pi+2\pi)[/tex]
[tex]\qquad C = \dfrac{1}{4}\cdot 24\pi[/tex]
[tex]\qquad \boxed{C = 6\pi \;\text{cm}}.[/tex]

---

Solução elaborada pelos Moderadores do Blog.