 |
Com base no que já estudamos na Sala introdutória, começamos esta Sala definindo funções exponenciais. |
► [tex]f(x)=7^x.[/tex]
► [tex]g(x)=\left(\dfrac{1}{2} \right)^x.[/tex]
► [tex]h(x)=(\sqrt{6})^x.[/tex]
As restrições [tex]a\gt 0[/tex] e [tex]a\neq 1[/tex] são necessárias. De fato, quando [tex]a=1[/tex], a função [tex]f(x)=1^x=1[/tex] é a função constante igual a [tex]1[/tex]. Quando [tex]a=0[/tex], a função [tex]f(x)=0^x[/tex] não está definida para valores negativos de [tex]x[/tex]. Por exemplo, quando [tex]x=-1[/tex], temos [tex]0^{-1}=\dfrac{1}{0^{1}}=\dfrac{1}{0}[/tex], o que é não está definido no conjunto dos números reais. Quando [tex]a\lt 0[/tex], a função não estaria definida em muitos valores de [tex]x[/tex]. Por exemplo, quando [tex]a=-3[/tex] e [tex]x=\dfrac{1}{2}[/tex] teríamos [tex]f(x)=(-3)^{\frac{1}{2}}=\sqrt{-3}[/tex], e sabemos que não existe raiz quadrada de números negativos no conjunto dos números reais.
Gráfico da Função Exponencial
Nesta seção, iremos estudar o gráfico de funções exponenciais. Usar o gráfico de uma função é sempre uma forma muito eficiente de apresentar as principais características de um fenômeno modelado por esta função. No caso da função exponencial, esses gráficos se separam em dois grupos com características similares, dependendo de ocorrer [tex]a\gt 1[/tex] ou [tex]0\lt a \lt 1[/tex]. Vejamos um exemplar de cada um desses grupos.
► [tex]f: \mathbb{R} \to \mathbb{R}[/tex] dada por [tex]f(x)=2^x[/tex]. Podemos usar nossos conhecimentos envolvendo exponenciação para obter vários pares de pontos [tex](x,f(x))[/tex], como mostrado na tabela. O gráfico de [tex]f[/tex] é a curva mostrada na figura e é conhecido como curva exponencial. O leitor pode calcular mais pontos, com a ajuda de uma calculadora científica, e constatar que, de fato, essa curva é o conjunto dos pontos [tex](x,f(x))[/tex].
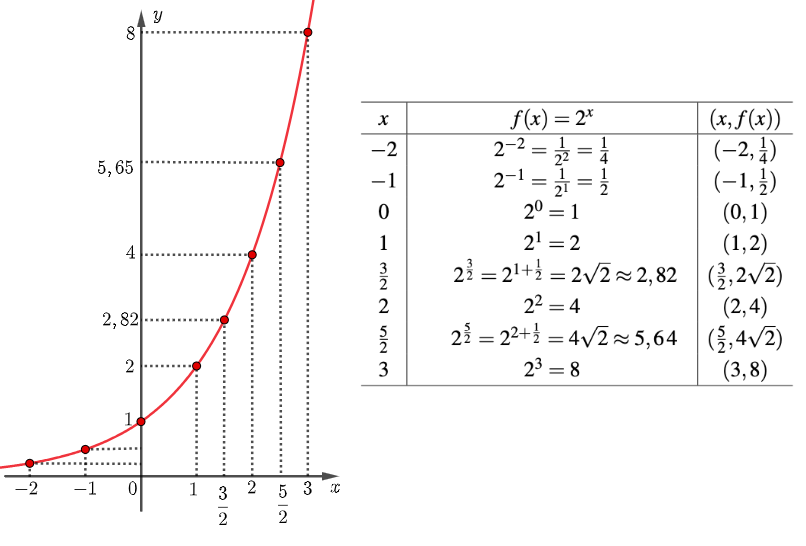
Observe que essa curva passa pelos pontos [tex](0,1)[/tex] e [tex](1,2)[/tex] e é uma função crescente, ou seja, à medida que os valores de [tex]x[/tex] aumentam, os valores de [tex]f(x)[/tex] também aumentam. Assim, se [tex]x_1\lt x_2[/tex], então [tex]2^{x_1}\lt 2^{x_2}[/tex]. Observe também que [tex]f(x)\gt 0[/tex], para qualquer [tex]x\in \mathbb{R}.[/tex]
► [tex]g: \mathbb{R} \to \mathbb{R}[/tex] dada por [tex]g(x)=\left(\dfrac{1}{2}\right)^x[/tex]. Poderíamos usar nossos conhecimentos envolvendo exponenciação para obter vários pares de pontos [tex](x,g(x))[/tex], como no exemplo anterior. Entretanto, observe que pela propriedade operatória (4) e a definição de potência com expoente negativo, temos
[tex]g(x)=\left(\dfrac{1}{2}\right)^x=\dfrac{1^x}{2^x}=\dfrac{1}{2^x}=2^{-x}=f(-x)[/tex].
Assim, o ponto [tex](x, g(x))[/tex] é o simétrico (espelhado) em relação ao eixo [tex]y[/tex] do ponto [tex](-x,f(-x))[/tex] e podemos usar os pontos do gráfico anterior para construir o gráfico de [tex]g[/tex]:
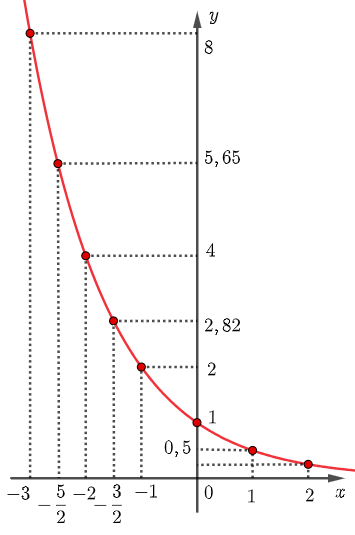
Novamente o leitor pode calcular mais pontos, com a ajuda de uma calculadora científica, e constatar que, de fato, essa curva é o conjunto dos pontos [tex](x,g(x))[/tex].
Observe que essa curva passa pelos pontos [tex](0,1)[/tex] e [tex](1,\frac{1}{2})[/tex] e é uma função decrescente, ou seja, à medida que os valores de [tex]x[/tex] aumentam os valores de [tex]g(x)[/tex] diminuem. Assim, se [tex]x_1\lt x_2[/tex], então [tex]\left(\frac{1}{2} \right)^{x_1}\gt \left(\frac{1}{2} \right)^{x_2}[/tex]. Observe novamente que [tex]g(x)\gt 0[/tex] para qualquer [tex]x\in \mathbb{R}[/tex].
► Quando [tex]a\gt 1[/tex], a função exponencial [tex]f(x)=a^x[/tex] é crescente, isto é, se [tex]x_1\lt x_2[/tex], então [tex]a^{x_1} \lt a^{x_2}[/tex].
► Quando [tex]0\lt a\lt 1[/tex], a função exponencial [tex]f(x)=a^x[/tex] é decrescente, isto é, se [tex]x_1\lt x_2[/tex], então [tex]a^{x_1} \gt a^{x_2}[/tex].
► O gráfico de [tex]f(x)=a^x[/tex] sempre contém os pontos [tex](0,1)[/tex] e [tex](1,a)[/tex].
► Independemente de termos [tex]0\lt a \lt 1[/tex] ou [tex]a\gt 1[/tex], a função [tex]f(x)=a^x[/tex] nunca assume valores negativos, isto é, para qualquer [tex]x\in \mathbb{R}[/tex], temos [tex]f(x)\gt 0[/tex].
Equações Exponenciais
O fato de uma função exponencial [tex]f(x)=a^x[/tex] ser sempre crescente ou sempre decrescente ajuda na resolução de algumas equações exponenciais, que são equações que apresentam a incógnita no expoente.
Consideremos a função exponencial [tex]f(x)=a^x[/tex] e dois números reais [tex]u[/tex] e [tex]v[/tex] que vamos supor respeitar [tex]u\lt v[/tex] (o caso [tex]u\gt v[/tex] é semelhante). Como esta função deve ser apenas crescente ou apenas decrescente, então [tex]a^u \lt a^v[/tex] (no caso [tex]a\gt 1[/tex]) ou [tex]a^u \gt a^v[/tex] (no caso [tex]0\lt a\lt 1[/tex]). Logo, quando [tex]a^u=a^v[/tex], a única possibilidade é que [tex]u=v[/tex]. Dessa forma:
[tex]a^u=a^v \ \ \Leftrightarrow \ \ u=v.[/tex]
Algumas pessoas, de maneira informal, escrevem essa propriedade “cortando as bases”:
[tex]\cancel{a}^u=\cancel{a}^v \ \ \Leftrightarrow \ \ u=v.[/tex]
Essa escrita não é muito precisa, embora o resultado seja correto nas condições que apresentamos acima. Esse fato auxilia na resolução das equações exponenciais em que ambos os membros podem ser escritos como potências de mesma base. Vejamos essa técnica sendo aplicada na resolução das equações exponenciais dos exemplos abaixo.
Exemplo 1: [tex]3^{x+1}=27.[/tex]
|
|
Exemplo 2: [tex]25^{2x+1}=125^{-x+2}.[/tex]
|
|
Exemplo 3: [tex]13^{x^2-9}=1.[/tex]
|
|
Exemplo 4: [tex]3^{x}=20.[/tex]
|
|
Exemplo 5: [tex]49^{x}-6\cdot 7^x-7=0.[/tex]
|
|
Crescimento e decrescimento exponencial
Funções [tex]f:\mathbb{R} \to \mathbb{R}[/tex] da forma [tex]f(x)=C a^x,[/tex] em que [tex]C[/tex] denota uma quantidade constante real e positiva, são conhecidas como funções do tipo exponencial. Vejam que se trata de uma função exponencial multiplicada por uma constante.
Essas funções são extremamente úteis para modelar fenômenos nos quais uma quantidade varia ao longo do tempo de maneira específica, a qual descreveremos a seguir. No instante de tempo [tex]x[/tex], vamos denotar essa quantidade por [tex]Q(x)[/tex]. Suponhamos que essa quantidade é positiva no início, ou seja, [tex]Q(0)\gt 0[/tex], e varia com o passar do tempo de forma que, durante cada unidade de tempo,
[tex]Q(x+1)=Q(x)+rQ(x)=Q(x)\cdot (1+r), [/tex]
em que [tex]r>-1[/tex] e [tex]r\neq 0[/tex] é um número real constante.
Em palavras: o valor da quantidade no final de uma unidade de tempo é o seu valor no início da unidade de tempo acrescido de uma fração fixa [tex]r[/tex] desta quantidade no início do intervalo. O número [tex]r[/tex] é conhecido como taxa de crescimento relativo e, na descrição de muitos problemas, é comumente apresentado na forma de porcentagem. Quando [tex]-1\lt r\lt 0[/tex], dizemos que a quantidade [tex]Q[/tex] apresenta um decaimento exponencial e, quando [tex] r\gt 0[/tex], dizemos que a quantidade [tex]Q[/tex] apresenta um crescimento exponencial.
Observemos como se comportam os valores da quantidade [tex]Q[/tex] com o passar do tempo:
[tex]\begin{array}{c|c}
\hline
x & Q(x)\\
\hline
{\color{red}1} & Q(1)=Q(0)\cdot(1+r)=Q(0)\cdot(1+r)^{\color{red}1}\\
{\color{red}2} & Q(2)=Q(1)\cdot(1+r)=Q(0)\cdot(1+r)\cdot(1+r)=Q(0)\cdot(1+r)^{\color{red}2}\\
{\color{red}3} & Q(3)=Q(2)\cdot(1+r)=Q(0)\cdot(1+r)^2\cdot(1+r)=Q(0)\cdot(1+r)^{\color{red}3}\\
\vdots & \vdots \\
\ {\color{red}n} & Q(n)=Q(0)\cdot(1+r)^{\color{red}n}\\
\hline
\end{array}
[/tex]
Assim, para medidas de tempo [tex]x[/tex] sendo um número natural positivo, a quantidade [tex]Q(x)[/tex] é uma função do tipo exponencial [tex]Q(x)=Ca^x[/tex], com [tex]C=Q(0)[/tex] e [tex]a=1+r[/tex]. Quando o tempo [tex]x[/tex] for um número real qualquer e a existência da quantidade [tex]Q(x)[/tex] fizer sentido, ela ainda será dada pela função do tipo exponencial [tex]Q(x)=Ca^x[/tex]. Isso será ilustrado nas aplicações que descreveremos a seguir.
Capitalização Composta
No regime de capitalização composta, um montante inicial [tex]C[/tex] de dinheiro, conhecido como capital, é aplicado ou emprestado, com uma taxa de juros ou de rendimento [tex]i[/tex] (aqui expresso na forma decimal) por período de tempo.

Nesse regime, os juros ou rendimentos são calculados no final de cada período e adicionados ao montante inicial, formando um novo montante sobre o qual os juros ou rendimentos do período seguinte serão calculados. De modo geral, o montante [tex]M(n+1)[/tex] ao final do período de ordem [tex]n+1[/tex] é o montante ao final do período anterior, [tex]M(n)[/tex], acrescido dos juros ou rendimentos [tex]iM(n)[/tex], ou seja,
[tex]M(n+1)=M(n)+iM(n)=M(n)\cdot(1+i).[/tex]
Assim, o valor do montante [tex]M(n)[/tex] após [tex]n[/tex] períodos pode ser expresso como uma função do número de períodos através de uma função do tipo exponencial:
[tex]M(n)=M(0)\cdot(1+i)^n=C(1+i)^n[/tex],
em que [tex]C[/tex] é o montante inicial, [tex]n[/tex] é o número de períodos e [tex]i[/tex] é a taxa de juros ou rendimentos por período.
Problema: Uma pessoa aplicou [tex]R\$\, 100 [/tex] mil na caderneta de poupança, que rendeu [tex]1\%[/tex] ao mês ao longo de um ano (lembre-se de que os juros são cumulativos). Ao fim do referido ano, essa pessoa tinha [tex]M[/tex] reais na caderneta de poupança, sem ter feito outro depósito além do inicial nem realizado saque. Calcule o valor de [tex]M[/tex].
|
|
Decaimento radioativo e a cronologia do carbono
As substâncias químicas capazes de emitir radiações são conhecidas como radioativas. A quantidade de matéria radioativa de um corpo diminui com o passar do tempo e isto se deve ao fato de que, quando um átomo emite radiação, ele se transforma em um átomo não radioativo. Mas o decaimento da matéria radioativa não acontece desordenadamente; isto é um fato extraordinário e com muitas aplicações. Foi comprovado que a cada substância radioativa está associado um período de tempo conhecido como meia-vida da substância tal que qualquer quantidade [tex]Q[/tex] dessa substância se reduzirá à metade após uma meia-vida.
Isto significa que a quantidade [tex]Q(n+1)[/tex] de matéria radioativa após [tex]n+1[/tex] meias-vidas de uma substância é a quantidade de matéria radioativa [tex]Q(n)[/tex] após [tex]n[/tex] meias-vidas, diminuída da metade dessa quantidade, ou seja,
[tex]Q(n+1)=Q(n)-0,5Q(n)=0,5Q(n)[/tex].
Observe que, neste caso, temos [tex]r=-0,5[/tex], e disso decorre a terminologia decaimento radioativo.
Assim, a quantidade de matéria radioativa [tex]Q(n)[/tex] após [tex]n[/tex] meias-vidas pode ser expressa como uma função do número de meias- vidas pela função do tipo exponencial
[tex]Q(n)=Q(0)\cdot (0,5)^n,[/tex]
em que [tex]Q(0)[/tex] é a quantidade de matéria radioativa inicial e [tex]n[/tex] é o número de meias-vidas que se passaram.
Vejamos uma aplicação muito interessante do conceito de meia-vida de elementos radioativos para a datação de fósseis encontrados na natureza.
A tabela abaixo fornece a meia-vida de alguns elementos químicos radioativos:
[tex]
\begin{array}{c|c}
\hline
\text{Urânio-238} & 4,5 \text{ bilhões de anos }\\
\text{Urânio-234} & 246 \text{ mil anos }\\
\text{Tório-230} & 76 \text{ mil anos }\\
{\color{green}\text{Carbono-14}} & {\color{green} 5730 \text{ anos }}\\
\text{Rádio-226} & 1600 \text{ anos }\\
\text{Chumbo-210} & 22 \text{ anos }\\
\text{Polônio-210} & 138 \text{ dias }\\
\text{Chumbo-214} & 27 \text{ minutos }\\
\text{Polônio-218} & 3 \text{ minutos }\\
\hline
\end{array}
[/tex]
Um elemento radioativo com meia-vida adequada para datar eventos na escala da história humana é o carbono-14. Vejamos como funciona esse “relógio radioativo”.
Na atmosfera, a concentração do carbono-14 em relação ao total de carbono é constante. Os seres vivos obtêm seu carbono direta ou indiretamente da atmosfera, por fotossíntese, por consumo de outros seres vivos que adquiriram o carbono por fotossíntese, etc. Assim, todos os seres vivos têm uma concentração de carbono-14 aproximadamente igual à da atmosfera enquanto estão vivos, pois estão continuamente trocando carbono com o ambiente. No momento da morte, a fotossíntese ou consumo de C-14 cessa e a concentração por grama começa a decair devido à radiação do C-14. Os outros outros isótopos de carbono permanecem constantes, enquanto o C-14 se desintegra ao longo do tempo. A cada [tex]5\,730[/tex] anos, a concentração de C-14 sofre uma queda de [tex]50\%[/tex]. Dessa forma, quando encontramos um fóssil, a medida da concentração de carbono-14 por grama informa, aproximadamente, o tempo que passou desde a morte desse ser vivo, isto é, quanto menor a concentração, mais tempo se passou desde a sua morte. Esse método para datar a idade de fósseis é conhecido como cronologia do carbono.
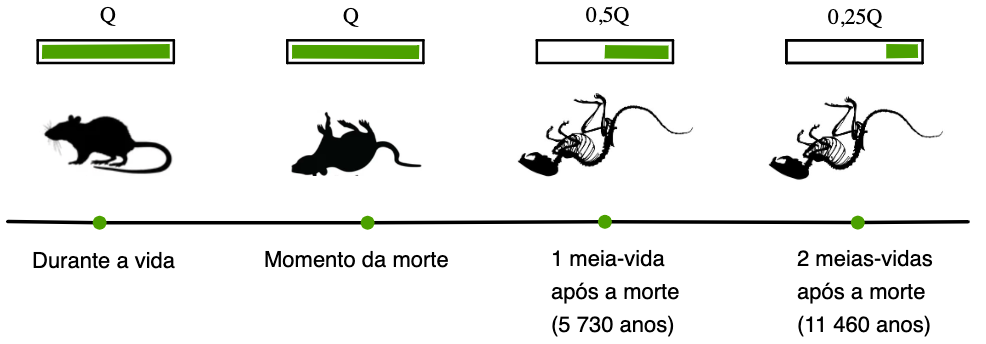
Problema: Suponha que um determinado animal possui, quando vivo, uma quantidade aproximada de [tex]Q[/tex] gramas de carbono-14, uma substância radioativa, com meia-vida de [tex]5 \ 730[/tex] anos. Quando este animal morre, a absorção dessa substância cessa e a quantidade começa a diminuir com o passar do tempo. Um fóssil desse animal foi encontrado com uma quantidade de [tex]0,3Q[/tex] gramas dessa substância radioativa. Estime, aproximadamente, a idade do fóssil.
|
|
Crescimento de populações
Imagine uma população, que pode ser de microorganismos, animais, pessoas ou mesmo as pessoas que estão contaminadas por uma doença contagiosa, com uma população inicial de [tex]P(0)[/tex] indivíduos, e que está variando a uma taxa relativa de [tex]r[/tex] por período de tempo. Ou seja, o tamanho da população [tex]P(n+1) [/tex] ao final do período de tempo [tex]n+1[/tex] é o tamanho da população [tex]P(n)[/tex] no início do período de tempo [tex]n+1[/tex] mais uma fração [tex]r[/tex] da população no início do período de tempo [tex]n+1[/tex]. Assim,
[tex]P(n+1)=P(n)+rP(n)[/tex].
Portanto, a população [tex]P(n)[/tex] após [tex]n[/tex] períodos de tempo pode ser expressa como função do número de períodos pela função do tipo exponencial,
[tex]P(n)=P(0)\cdot (1+r)^n,[/tex]
em que [tex]P(0)[/tex] é a população inicial e [tex]n[/tex] é o número de períodos de tempo que se passaram.
Problema: (UFMG-MG) A população de uma colônia da bactéria E.coli dobra a cada [tex]20[/tex] minutos.
Em um experimento, colocou-se inicialmente, em um tubo de ensaio, uma amostra com [tex]1000[/tex] bactérias por mililitro. No final do experimento, obteve-se um total de [tex]4,096 \cdot 10^6[/tex] bactérias por mililitro. Calcule o tempo do experimento.
|
|
Equipe COM – OBMEP
Janeiro de 2025
