Apresentação
Durante o ensino da Matemática escolar, geralmente, a única geometria que nos é apresentada é a euclidiana. As formas geométricas de polígonos e poliedros, suas propriedades e suas características são utilizadas para modelar e compreender diversos elementos que aparecem em nosso cotidiano. Além disso, historicamente, as construções e criações realizadas pelo homem possuem, em sua grande maioria, formas geométricas euclidianas. Alguns exemplos são as pirâmides do Egito, edifícios e celulares. Ainda no ambiente escolar, em diversas atividades e exercícios, tentamos, matematicamente, reduzir alguns objetos da natureza às formas geométricas simples. Em algumas situações, essa estratégia é muito eficaz, como a da aproximação da superfície terrestre por uma esfera, órbitas celestes por elipses e lançamento oblíquo de um objeto por parábolas.
Mas é claro que a existem diversos elementos e objetos na natureza que não podem ser descritos pela geometria euclidiana. Na verdade, a maioria das formas que aparecem ao nosso redor não são regulares, pelo contrário, são, em geral, complexas e irregulares. É o caso, por exemplo, das nuvens, montanhas e relâmpagos.
Em 1983, o matemático francês, nascido na Polônia, Benoit Mandelbrot (1924 – 2010) escreveu, em seu livro The Fractal Geometry of Nature, que: “Nuvens não são esferas, montanhas não são cones, continentes não são círculos, troncos de árvores não são suaves e nem o relâmpago viaja em linha reta.”

Mandelbrot era um exímio geômetra e se incomodava com a algebrização da Matemática praticada pela École Polytechique da França. Esse foi um dos motivos da sua ida para os Estados Unidos, para trabalhar no Instituto de Pesquisa James Watson da International Business Machines Corporation (IBM). No Instituto, aperfeiçoando-se nos estudos de computação gráfica, Mandelbrot conseguiu criar e explicar, a partir de regras simples, formas geométricas complexas. Seus estudos contribuíram para diversas áreas como Medicina, Geologia, Engenharia e as Ciências Sociais.
O objetivo desta sala é apresentar e propor atividades com figuras geométricas não tradicionais conhecidas como Fractais. O termo Geometria Fractal foi criado em 1975 por Mandelbrot e é uma tentativa de estudar alguns objetos e fenômenos para os quais a geometria euclidiana não é suficiente.
Um pouco sobre fractais
Entre o final do século XIX e início do XX, a ideia dos fractais foi difundida no trabalho de alguns cientistas. Nesse trabalho, foram constatados alguns objetos que ficaram denominados como “monstros matemáticos”. Alguns deles são:
Conjunto de Cantor
O matemático Georg Cantor (1845 – 1918) definiu, como o Conjunto de Cantor, um subconjunto fechado do intervalo [tex][0, 1][/tex], obtido como complementar de uma reunião de intervalos abertos, do seguinte modo:
Dividimos o intervalo [tex][0, 1][/tex] em três partes iguais e desconsideramos o terço médio, isto é, o intervalo [tex] \left]\dfrac{1}{3}, \dfrac{2}{3} \right[ [/tex]. Em seguida, repete-se esse procedimento para os dois intervalos restantes, [tex] \left[0, \dfrac{1}{3}\right] [/tex] e [tex] \left[\dfrac{2}{3}, 1 \right] [/tex], repetindo este processo etapa a etapa, infinitamente.
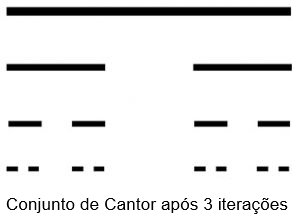
O conjunto [tex]C[/tex] obtido após infinitas iterações é o que se chama Conjunto de Cantor ou ainda Poeira de Cantor.
Curva de Koch
Uma outra construção, proposta pelo matemático sueco Helge Von Koch (1870 – 1924), também é baseada na divisão de um segmento inicial em três partes iguais. Porém, o terço médio será substituído por um triângulo equilátero sem a base. A imagem a seguir representa apenas as quatro primeiras iterações, a curva de Koch é obtida após infinitas iterações.
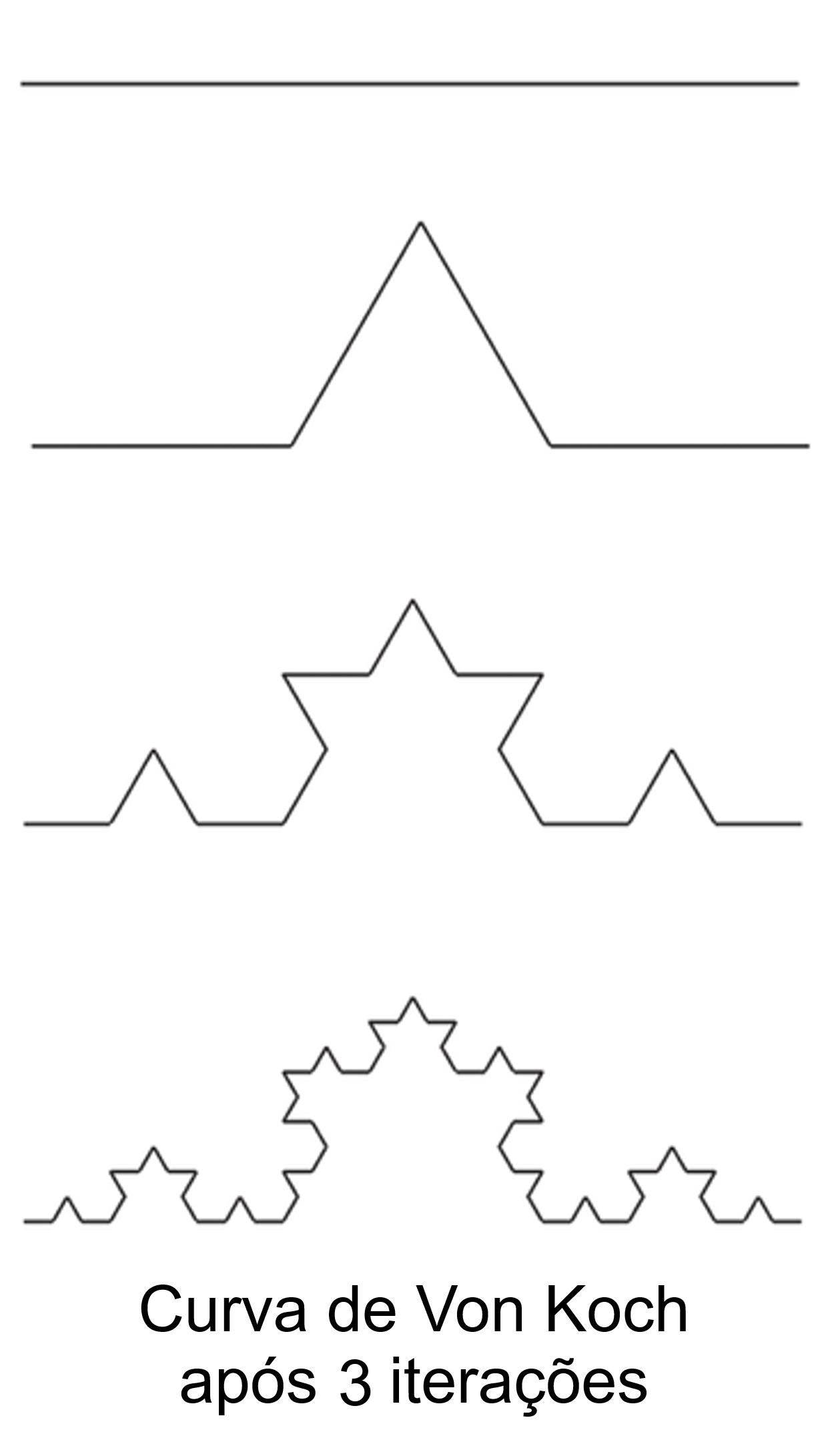
Triângulo de Sierpinski
Em 1915, o matemático polonês, Waclaw Sierpinski (1882 – 1969) descreveu o seguinte procedimento:
Partindo de um triângulo equilátero, remova o triângulo equilátero definido pelos pontos médios dos lados. Repita o processo para os outros três triângulos equiláteros que permaneceram e assim sucessivamente. O triângulo de Sierpinski é obtido após infinitas iterações.

É de extrema importância ressaltar que, quando esses objetos matemáticos foram propostos pelos matemáticos, ainda não existia o conceito de fractal. Apenas após os trabalhos de Mandelbrot surgiram teorias para que todos fossem enquadrados em um mesmo estudo. Foi através do conjunto de Cantor, por exemplo, que Mandelbrot conseguiu solucionar alguns problemas de transmissão de dados de um computador para outro, via linha telefônica. Reprogramando os computadores, tornou a comunicação muito mais viável.
Interessante, não é??? Mas… o que é um fractal?
De uma maneira bem simples, fractais são elementos gerados pela repetição de um mesmo processo (iteração/recursão), apresentando autossimilaridade e complexidade infinita. Um objeto é dito autossimilar se é semelhante a uma parte de si mesmo. Essa geometria vem se consolidando nos últimos anos com o desenvolvimento da tecnologia computacional e com auxílio de novas teorias nas áreas da Física, Biologia, Astronomia e Matemática. Citamos algumas aplicações atuais dos fractais:
- Cidades fractais: Algumas cidades tendem a crescer em padrões fractais ao longo do tempo e são chamadas de cidades fractais. À medida que uma grande cidade fractal absorve suas cidades e vilas vizinhas, o padrão desenvolvido se assemelha a uma estrutura autossimilar que parece aleatória a princípio, mas é uma rede dinâmica que pode provar ser mais eficiente do que as cidades modernas “pré-planejadas”.
- Medicina fractal: O conhecimento de fractais é especialmente útil em diagnósticos médicos, incluindo câncer. Como as células saudáveis dos vasos sanguíneos humanos geralmente crescem em um padrão fractal ordenado, as células cancerosas, que crescem de forma anormal, tornam-se mais fáceis de detectar. Essa forma de análise fractal torna muito mais fácil distinguir entre células saudáveis e sinais de preocupação.
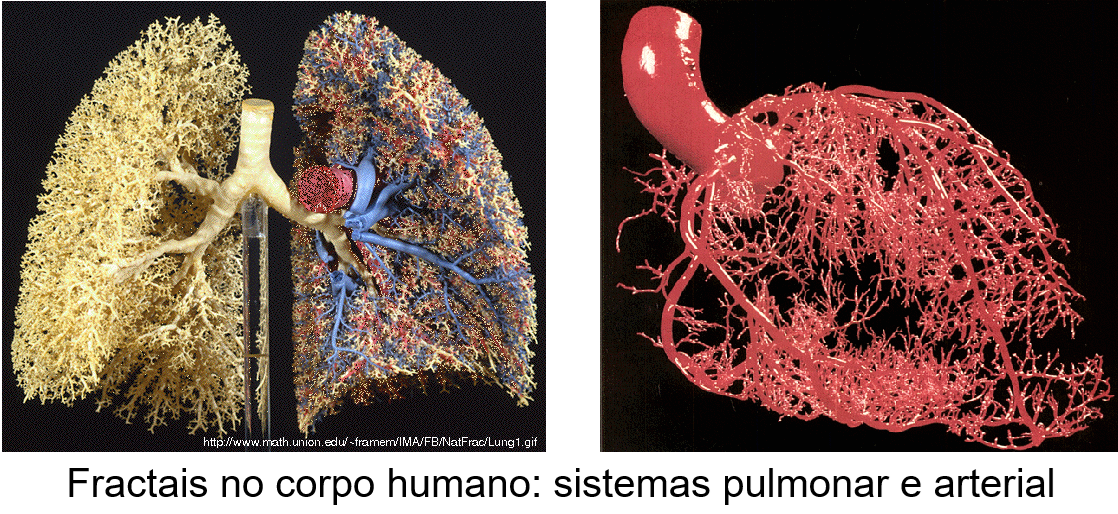
- Compressão e resolução de imagem: Como os fractais nos permitem transmitir padrões aparentemente aleatórios com poucos dados, trabalhar com resolução de imagem e até mesmo criação de modelo 3D torna-se extremamente eficiente em dados usando codificação de imagem fractal (FIC, de fractal image coding, em inglês) e outros aplicativos.
- Antenas: A natureza tipicamente autossimilar dos fractais também é útil na criação e operação de antenas. Curvas como a curva de Hilbert podem ser usadas para projetar antenas de alto desempenho.
- Arte: A gama de regras que governam a criação fractal, do simplista ao complexo, é totalmente atraente para os artistas.

|
Agora que já sabemos um pouquinho sobre fractais, vamos realizar algumas atividades?
Em alguns momentos será necessário o conhecimento das propriedades das progressões geométricas. Para relembrá-las, clique AQUI.
|
Atividades
Atividade 1: Fractal Degraus Centrais
Você conhece uma escada não é mesmo? E se eu disser que você pode construir uma escada um pouco diferente com infinitos degraus? Interessante, não é? Então, para essa atividade, você deve seguir as instruções abaixo com os seguintes materiais: uma folha de papel, tesoura, régua e lápis.
1- Dobre a folha ao meio (ao longo do seu menor lado) fazendo um vinco na dobra;

2-Utilize a régua, o lápis e a tesoura e faça dois cortes verticais e simétricos de modo que cada corte chegue à metade do papel como na figura;

3- A linha tracejada representa onde será feita uma dobra;

4- Dobre o corte, como na figura, até que as extremidades do corte e da folha estejam sobrepostas;

5- Faça um segundo vinco na base inferior dessa dobra;

Esta é a primeira iteração do fractal.
6- Desfaça a dobra para a posição inicial e puxe a extremidade do corte para o interior da folha. Faça mais um vinco com a folha dobrada até que a mesma fique, quando aberta, como no desenho abaixo:
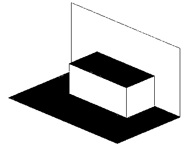
7- Dobre o papel novamente com o primeiro degrau em seu interior;

8- Faça novamente dois cortes verticais e simétricos (idem ao passo 2) como na figura;
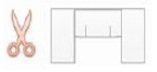
9- Marque a dobra;
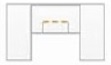
10- Dobre a folha até que as extremidades do novo corte e da folha estejam sobrepostas (conforme a figura abaixo) fazendo mais um vinco. Está pronta a segunda iteração;
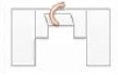
11- Desfaça as dobras para a posição inicial e puxe os dois novos centros para o interior da folha. Faça mais um vinco com a folha dobrada até que a mesma fique como no desenho abaixo:
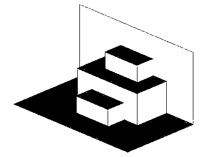
12- Repetindo essas etapas algumas vezes teremos o nosso cartão fractal degraus centrais.

Caso não tenha conseguido, assista ao vídeo:

Com os nossos materiais utilizados, temos uma limitação na construção dos degraus. Contudo, matematicamente, podemos fazer uma infinidade de iterações.
Para a próxima atividade, suponha que seja possível fazer infinitas iterações.
Atividade 2: Explorando o cartão fractal degraus centrais
Agora que você já construiu sua escada, responda os itens a seguir:
a) Repare que ao fazer a primeira iteração, surgiu apenas um degrau. Na segunda iteração, surgiram mais dois degraus. Na terceira iteração, surgiram mais quatro degraus e assim sucessivamente. Quantos degraus surgirão na sexta iteração?
b) Seja [tex]n[/tex] o número de iterações feitas e [tex]d[/tex] o número de novos degraus no cartão. Qual a relação entre esses dois números?
c) Você conhece o nome da sequência numérica formada pelos números de novos degraus surgidos de acordo com o número [tex]n[/tex] de iterações [tex](1,2,4,8, \dots ,2^{n-1})[/tex]?
d) Qual é o número total de degraus ao ser feita a sétima iteração?
e) Admitindo que uma folha tem os lados medindo [tex]21[/tex] cm e [tex]30[/tex] cm, qual a altura do degrau da primeira iteração? E a altura de cada degrau da segunda iteração?

f) Ao medir a altura de apenas um degrau após cada iteração, qual seria a soma de todas essas alturas após infinitas iterações?
Atividade 3: Floco de neve de Koch
Em 1904, o sueco Helge Von Koch criou a curva de Von Koch que, tempos depois, deu origem ao “Floco de neve de Koch”.
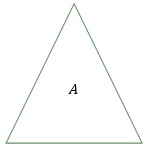
A construção inicia-se com um triângulo equilátero.
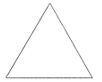
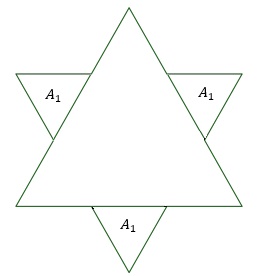
Na primeira iteração da construção, cada lado do triângulo é dividido em três segmentos congruentes e sobre o segmento central de cada lado é construído um novo triângulo equilátero, sem a base. Nessa primeira iteração, o polígono formado é semelhante ao polígono conhecido como a “Estrela de Davi” e possui [tex]12[/tex] lados.
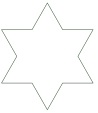
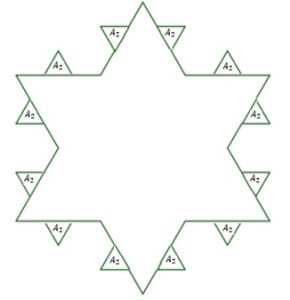
Repetindo o mesmo processo, temos a imagem da segunda iteração. Nessa etapa, o polígono possui [tex]48[/tex] lados.
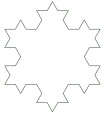
Refazendo o processo indefinidamente, construímos o fractal denominado Floco de neve de Koch.
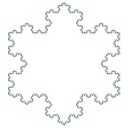
Agora que você já conhece a construção desse fractal, tente responder aos itens a seguir.
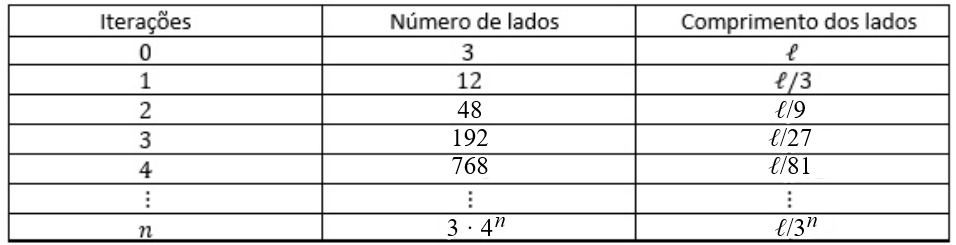
a) Sendo [tex]\ell[/tex] o comprimento do triângulo equilátero da figura inicial e [tex]n[/tex] o número de iterações do fractal, preencha a tabela abaixo:

b) Pelo item a, podemos notar que o número de lados tende a aumentar (tende para infinito) e o comprimento dos lados tende a diminuir (tende para zero) de acordo com aumento das iterações. Encontre uma expressão para o perímetro do Floco de neve em função do número [tex]n[/tex] de iterações e conclua como se comporta essa expressão (tende a aumentar ou tende a diminuir?).
c) E o que ocorre com a área do floco de neve? Tente encontrar uma expressão para área e conclua como ela se comporta.
Bem interessante o que acabamos de concluir… Apesar do perímetro tender ao infinito, a área é finita e conseguimos encontrar seu valor.
Atividade 4: Triângulo de Sierpinsk
Outro cartão que pode ser explorado é o cartão Triângulo de Sierpinski. Sua estrutura triangular pode ser comparada ao conjunto fractal que leva o mesmo nome.
Assista este vídeo e tente construir esse cartão:


Resolva o problema abaixo, que aborda o Triângulo de Sierpinsk:
O triângulo de Sierpinski, uma das formas elementares da geometria fractal, pode ser obtido por meio dos seguintes passos:
1. comece com um triângulo equilátero (figura 1);
2. construa um triângulo em que cada lado tenha a metade do tamanho do lado do triângulo anterior e faça três cópias;
3. posicione essas cópias de maneira que cada triângulo tenha um vértice comum com um dos vértices de cada um dos outros dois triângulos, conforme ilustra a figura 2;
4. repita sucessivamente os passos 2 e 3 para cada cópia dos triângulos obtidos no passo 3 (figura 3).
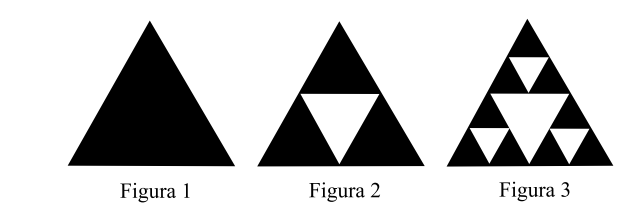
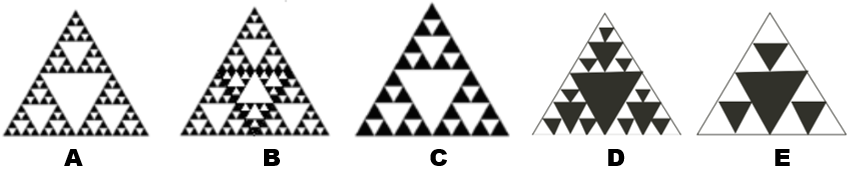
De acordo com o procedimento descrito, a figura 4 da sequência apresentada acima é
O vídeo a seguir pode ajudar com a resposta da questão.
Você sabia? Se na representação do Triângulo de Pascal como um triângulo isósceles colorirmos as entradas contendo números ímpares com uma cor e as entradas contendo números pares com outra, o resultado será um triângulo com o mesmo padrão do Triângulo de Sierpinski. Para aprender mais, consulte esta página do nosso Blog.
Bom trabalho, pessoal!
Equipe COM – OBMEP
[1]CÔRTES, I. Geometria Fractal no Ensino Médio: Teoria e Prática. TCC (Mestrado) – Universidade Federal do Estado do Rio de Janeiro (UNIRIO).
[2] Departamento de Física Aplicada. Disponível em: https://portal.if.usp.br/fap/. Acesso em: 6 set. 2024.
[3] Matemática Discreta: Coleção Profmat – Augusto César Morgado; Paulo Cesar Pinto Carvalho.
[4] Notas de aulas do professor Cleber Gouvêa Fernandes.
[5] Top 5 applications of fractals. Disponível em: https://uwaterloo.ca/math/news/top-5-applications-fractals. Acesso em: 6 set. 2024.
[6] Valério, B. O uso de fractais na sala de aula por meio de atividades investigativas. Oficina 7- IME-USP.