Problema
(Indicado a partir do 8º ano do E. F.)
O Quociente Isoperimétrico é um índice usado para medir o quanto uma figura planar, que possui perímetro e área, é redonda. Dada uma figura [tex]F[/tex] com área [tex]A_f[/tex] e perímetro [tex]P_f[/tex], o Quociente Isoperimétrico [tex]I_f[/tex] para esta figura é calculado por
[tex]\qquad I_f=\dfrac{4\pi A_f}{P_f^2}.[/tex]
Pode ser mostrado que, para qualquer figura [tex]F[/tex], tem-se [tex]0\lt I_f \leq 1[/tex] e que, quanto mais redonda for a figura, mais próximo de [tex]1[/tex] estará o índice [tex]I_f[/tex].
a) Calcule o valor do Quociente Isoperimétrico para um círculo.
b) Use o Quociente Isoperimétrico para classificar, do menos redondo ao mais redondo, um quadrado, um hexágono regular e um semicírculo. Use uma calculadora científica para calcular o valor das constantes envolvidas.
Solução
a) Um círculo [tex]C[/tex] de raio [tex]r[/tex] tem perímetro [tex]2\pi r[/tex] e área [tex]\pi r^2[/tex]. O Quociente Isoperimétrico para este círculo será então:
[tex]\qquad I_C=\dfrac{4 \pi (\pi r^2)}{(2 \pi r)^2}=\dfrac{4 \pi^2 r^2}{4 \pi^2 r^2}=1.[/tex]
Como esperado, o círculo é totalmente redondo.
b) Um quadrado [tex]Q[/tex] de lado [tex]l[/tex] possui perímetro [tex]4l[/tex] e área [tex]l^2[/tex]. Assim:
[tex]\qquad I_Q=\dfrac{4 \pi (l^2)}{(4 l)^2}=\dfrac{4 \pi l^2}{16 l^2}=\dfrac{\pi}{4}\approx 0,785.[/tex]
Um hexágono regular [tex]H[/tex] de lado [tex]l[/tex] possui perímetro [tex]6l[/tex] e área [tex]\qquad \dfrac{3\sqrt{3}l^2}{2}[/tex]. Assim:
[tex]\qquad I_H=\dfrac{4 \pi \dfrac{3\sqrt{3}l^2}{2}}{(6 l)^2}=\dfrac{12\pi \sqrt{3} l^2}{72 l^2}=\dfrac{\pi\sqrt{3}}{6}\approx 0,907.[/tex]
Um semicírculo [tex]S[/tex] de raio [tex]r[/tex] possui perímetro [tex]2r+\pi r[/tex] e área [tex]\dfrac{\pi r^2}{2}[/tex]. Assim:
[tex]\qquad I_S=\dfrac{4 \pi \dfrac{\pi r^2}{2}}{( 2r+\pi r)^2}=\dfrac{4 \pi^2 r^2}{2 (2+\pi)^2 r^2}=2\left( \dfrac{\pi}{2+\pi}\right)^2\approx 0,747.[/tex]
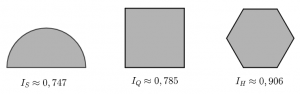
Dessa forma, a classificação do menos redondo para o mais redondo é: semicírculo, quadrado e hexágono.
Solução elaborada pelos Moderadores do Blog.
