Problema
(Indicado a partir do 1º ano do E. M.)
A comissão de formatura dos estudantes do 3° ano do Ensino Médio está fazendo alguns orçamentos para a realização de uma festa para [tex]480[/tex] convidados. Por exemplo, para a locação do salão de festas, eles receberam o seguinte orçamento: “Cada convidado presente na festa deve pagar [tex]R\$ \ 8,00[/tex] acrescidos de [tex]R\$ \ 0,10[/tex] por convidado ausente”.
Qual é o maior valor possível que se pode pagar pela locação desse salão? Nesse caso, quantos são os convidados que comparecerão à festa?
Extraído de Multiversos Matemática: Funções e suas aplicações.

Lembretes
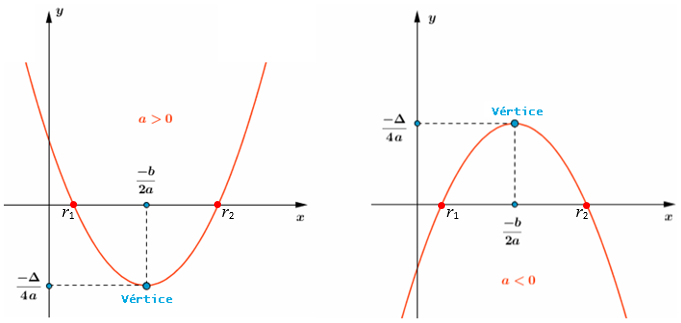
[tex]{\color{#800000}(1)}[/tex] O gráfico de uma função quadrática [tex]h:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]h(x)=ax^2+bx+c,\, a\not=0[/tex], é uma parábola com diretriz paralela ao eixo [tex]Ox[/tex], eixo de simetria paralelo ao eixo [tex]Oy[/tex], sendo sua concavidade voltada para cima se [tex]a\gt 0[/tex] e voltada para baixo se [tex]a\lt0[/tex].
[tex]{\color{#800000}(2)}[/tex] Se [tex]\Delta= b^2-4ac[/tex], as coordenadas do vértice da parábola do gráfico de [tex]h[/tex] são dadas por:
[tex]\qquad \qquad (x_v,y_v)=\bigg(\dfrac{-b}{2a},\dfrac{-\Delta}{4a}\bigg)[/tex],
sendo que [tex]x_v=\dfrac{-b}{2a}\, [/tex] e [tex]\, y_v=\dfrac{-\Delta}{4a}[/tex] indicam, respectivamente:
✓ o ponto de mínimo e o valor mínimo da função [tex]h[/tex], se a concavidade estiver voltada para cima;
✓ o ponto de máximo e o valor máximo da função [tex]h[/tex], se a concavidade estiver voltada para baixo.
Particularmente, se [tex]\Delta \gt 0[/tex], [tex]x_v[/tex] é a média entre as duas raízes de [tex]h[/tex]: [tex]x_v=\dfrac{r_1+r_2}{2}\, .[/tex]
Visualizem as informações fornecidas no lembrete [tex]{\color{#800000}(2)}[/tex], se [tex]\Delta \gt 0[/tex],
clicando no botão abaixo.
Solução
Suponhamos que [tex]x[/tex] convidados comparecerão à festa e [tex](480-x)[/tex] se ausentarão. Cada convidado deverá pagar
[tex]\qquad 8+0,1(480-x)=56-0,1x[/tex]
reais. Assim, o valor [tex]V(x)[/tex] pago pela locação será
[tex]\qquad V(x)=x(56-0,1x)=-0,1x^2+56x.[/tex]
Precisamos determinar o número de convidados [tex]x[/tex] que torna o valor pago [tex]V(x)[/tex] de locação máximo, ou seja, precisamos determinar as coordenadas do vértice [tex](x_v, y_v) [/tex] da parábola [tex]y=-0,1x^2+56x[/tex]. Assim, obtemos
[tex]\qquad x_v=\dfrac{-b}{2a}=\dfrac{-56}{-0,2}=280[/tex]
convidados e
[tex]\qquad y_v=\dfrac{-\Delta}{4a}=\dfrac{-56^2}{-0,4}=\dfrac{-3136}{-0,4}=7840[/tex]
reais. Logo, o maior valor possível que se pode pagar pela locação desse salão é [tex]7840[/tex] reais e ocorre quando comparecem à festa [tex]280[/tex] convidados.
Solução elaborada pelos Moderadores do Blog.