Problema
(Indicado a partir da 1ª Série do E. M.)
Um triângulo [tex]ABC[/tex] é dividido em [tex]4[/tex] partes por dois segmentos de reta, conforme mostrado abaixo. As áreas dos triângulos menores são [tex]1, 3[/tex] e [tex]3[/tex]. Qual é a área do triângulo [tex]ABC[/tex]?
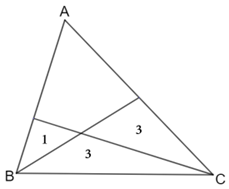
Extraído de Olimpíada Canguru [tex]2021[/tex] – Nível S.
Solução
Como os triângulos [tex]AME[/tex] e [tex]AMC[/tex] têm o vértice [tex]A[/tex] comum oposto às suas bases colineares [tex]EM[/tex] e [tex]MC[/tex], eles têm mesma altura relativa a essas bases. Então, essas bases têm comprimentos proporcionais às respectivas áreas dos triângulos [tex]AME[/tex] e [tex]AMC[/tex].
O mesmo ocorre com os triângulos [tex]BME[/tex] e [tex]BMC[/tex]. Logo, as áreas dos triângulos [tex]AME[/tex] e [tex]AMC[/tex] são proporcionais às áreas dos triângulos [tex]BME[/tex] e [tex]BMC[/tex], ou seja, [tex]\dfrac{x}{y+3}=\dfrac{1}{3} \qquad (I).[/tex]
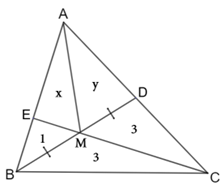
O segmento [tex]BD[/tex] está dividido ao meio pelo ponto [tex]M[/tex], pois os triângulos [tex]CMB[/tex] e [tex]CMD[/tex] possuem mesma área e mesma altura relativa às bases [tex]BM[/tex] e [tex]MD[/tex], respectivamente. Logo, as áreas dos triângulos [tex]AMB[/tex] e [tex]AMD[/tex] também possuem mesmo valor, ou seja, [tex]y=x+1[/tex]. Substituindo essa expressão em [tex](I)[/tex], vem:
[tex]\qquad \dfrac{x}{x+1+3}=\dfrac{1}{3}[/tex]
[tex]\qquad 3x=x+4 [/tex]
[tex]\qquad x=2.[/tex]
Assim, a área do triângulo [tex]ABC[/tex] é igual a [tex]1+3+3+2+3=12.[/tex]
Solução elaborada pelos Moderadores do Blog.
