O que é uma Transformação Geométrica?

|
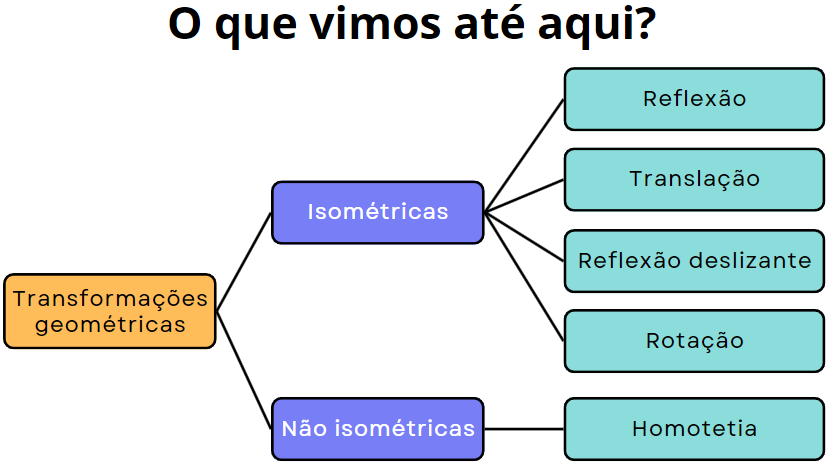
É uma aplicação bijetiva entre duas figuras geométricas, no mesmo plano ou em planos diferentes, onde a partir de uma figura geométrica original se forma outra geometricamente igual ou semelhante à primeira.
|
Isometrias
Uma Isometria é uma transformação geométrica que preserva distância entre pontos e amplitude dos ângulos. Em outras palavras, a figura original e a figura transformada são congruentes. Abaixo, vamos estudar os diferentes tipos de isometrias.
Reflexão
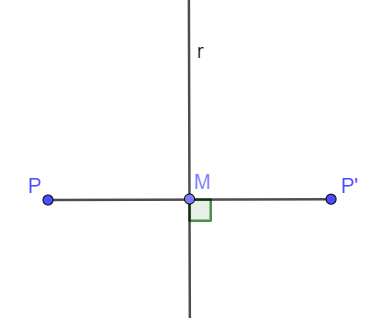
É uma transformação isométrica no plano, com eixo [tex]r[/tex], em que cada ponto [tex]P[/tex] corresponde a um ponto [tex]P’[/tex] de tal forma que:
- [tex]r[/tex] é o eixo de reflexão;
- [tex]P’[/tex] é o reflexo de [tex]P[/tex];
- O segmento [tex]PP’[/tex] é perpendicular ao eixo [tex]r[/tex];
- A distância de [tex]P[/tex] a [tex]r[/tex] é igual à distância de [tex]P’[/tex] a [tex]r[/tex], ou seja, [tex]\overline{PM}=\overline{P’M}.[/tex]
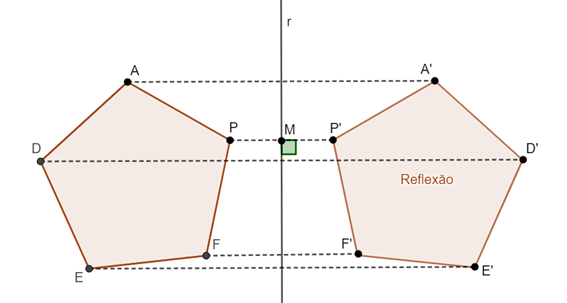
Uma figura e sua imagem obtida por reflexão são sempre congruentes e a figura original e sua reflexão sobrepõem-se ponto a ponto se dobradas uma sobre a outra pelo eixo [tex]r[/tex]. Além disso, a reflexão muda o sentido de abertura dos ângulos sem alterar sua amplitude.
No applet a seguir, reposicione qualquer vértice da figura da esquerda e observe o que ocorre com a figura da direita. Nessa atividade simples, você será capaz de perceber a reflexão de uma figura em relação a um eixo.
1) Aguarde o aplicativo carregar completamente.
2) Reposicione qualquer vértice da figura da esquerda e observe o que ocorre com a figura da direita.
3) Para reiniciar, clique nas setinhas que aparecem no canto superior direito do applet.
OBMEP_nzm, criado com o GeoGebra
Agora responda:
a) O quadrilátero [tex]A’B’C’D'[/tex] preserva as medidas lineares e angulares em relação ao quadrilátero [tex]ABCD[/tex]?
b) A transformação sofrida pelo quadrilátero [tex]ABCD[/tex] é ou não isométrica? Justifique.
Translação
É uma transformação isométrica no plano associada ao vetor [tex]\overrightarrow{u}[/tex], que faz corresponder a cada ponto [tex]P[/tex] da figura original um ponto [tex]P’[/tex] tal que [tex]\overrightarrow{u}= \overrightarrow{PP’}[/tex]. As translações conservam a direção e o comprimento de segmentos de reta e as amplitudes dos ângulos.
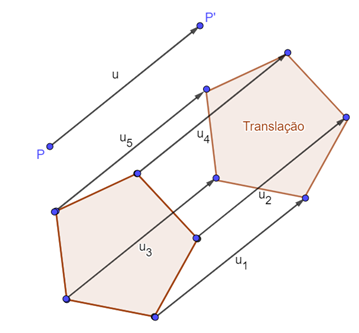
Na figura,
- [tex]\overrightarrow{u}[/tex] é o vetor de orientação da translação;
- [tex]\overrightarrow{u}=\overrightarrow{u_1}=\overrightarrow{u_2}=\overrightarrow{u_3}=\overrightarrow{u_4}=\overrightarrow{u_5}[/tex];
- A figura original e sua translação são congruentes.
No applet a seguir, qualquer vértice do triângulo [tex]ABC[/tex] pode ser reposicionado. Perceberemos que o vértice correspondente do triângulo [tex]FGH[/tex] passará pelo mesmo reposicionamento, gerando uma nova figura transladada em relação ao vetor [tex]\overrightarrow{DE}[/tex]. Além disso, você também pode reposicionar os pontos [tex]D[/tex] e [tex]E[/tex], modificando o vetor correspondente.
1) Aguarde o aplicativo carregar completamente.
2) Reposicione qualquer vértice do triângulo [tex]ABC[/tex] ou reposicione os pontos [tex]D[/tex] e [tex]E[/tex], modificando o vetor.
3) Para reiniciar, clique nas setinhas que aparecem no canto superior direito do applet.
OBMEP_nzm, criado com o GeoGebra
Agora responda:
a) A quais vértices do triângulo [tex]FGH[/tex] correspondem, respectivamente, cada vértice do triângulo [tex]ABC[/tex]?
b) Há alguma posição do triângulo [tex]ABC[/tex] de forma que sua área seja maior que a de seu correspondente transladado [tex]FGH[/tex]?
c) A transformação sofrida pelo triângulo [tex]ABC[/tex] é ou não isométrica? Justifique.
Reflexão Deslizante
É uma transformação geométrica que resulta de uma reflexão seguida de uma translação paralela ao eixo de reflexão.
- [tex]r[/tex] é o eixo de reflexão;
- [tex]\overrightarrow{u}[/tex] é o vetor de orientação da translação.
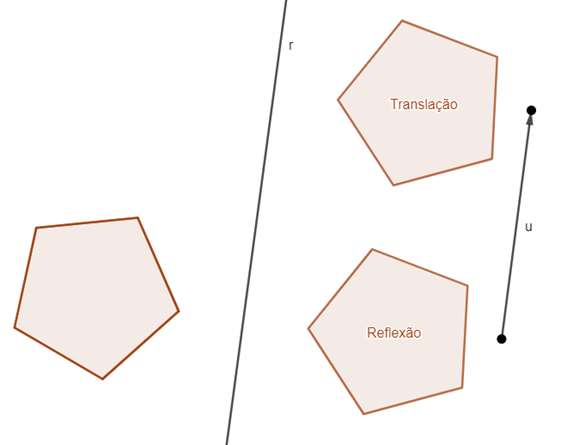
Você pode entender melhor ao assistir o seguinte vídeo:

No applet a seguir, temos o logo da OBMEP. Se você mover o ponto [tex]B[/tex], estará modificando o vetor da translação enquanto que, se mover o ponto [tex]C[/tex], estará modificando o eixo da reflexão.
1) Aguarde o aplicativo carregar completamente.
2) Mova os pontos [tex]B[/tex] ou [tex]C[/tex] para modificar o vetor de translação ou o eixo de reflexão, respectivamente.
3) Para reiniciar, clique nas setinhas que aparecem no canto superior direito do applet.
OBMEP_nzm, criado com o GeoGebra
Agora responda:
a) O que ocorreu ao movimentar o ponto [tex]B[/tex]?
b) O que ocorreu ao movimentar o ponto [tex]C[/tex]?
Rotação
É uma transformação Isométrica no plano com centro de rotação [tex]P[/tex] e amplitude [tex]\beta[/tex], onde cada ponto [tex]A[/tex] da figura original corresponde a um ponto [tex]A’[/tex] da figura rotacionada tal que:
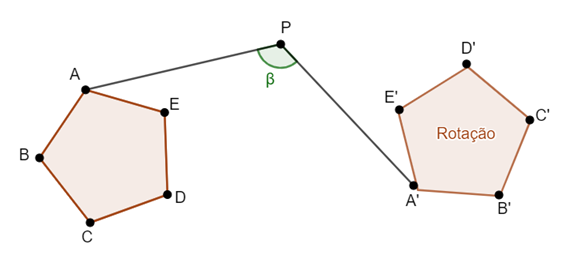
- [tex]P[/tex] é o centro de rotação;
- [tex]\beta[/tex] é a amplitude do ângulo de rotação;
- [tex]\overline{PA}=\overline{PA’}[/tex];
- [tex]A\hat{P}A’=\beta[/tex].
Na figura do exemplo, temos também [tex]B\hat{P}B’=\beta, C\hat{P}C’=\beta, D\hat{P}D’=\beta, E\hat{P}E’=\beta[/tex].
A rotação pode ter dois sentidos:
[tex]1^\circ[/tex] Positivo: quando a figura se move no sentido contrário ao dos ponteiros do relógio;
[tex]2^\circ[/tex] Negativo: quando a figura se move no mesmo sentido dos ponteiros do relógio. Na figura acima, a rotação é positiva.
No applet a seguir, aumente o valor do ângulo [tex]a[/tex] lentamente para ver o que ocorre com a figura.
1) Aguarde o aplicativo carregar completamente.
2) No controle deslizante, modifique o ângulo [tex]a[/tex] de rotação positiva. Você também pode movimentar os pontos [tex]A[/tex], [tex]B[/tex], [tex]C[/tex] e [tex]D[/tex] para modificar o quadrilátero, assim como movimento o ponto [tex]O[/tex], o centro de rotação.
3) Para reiniciar, clique nas setinhas que aparecem no canto superior direito do applet.
OBMEP_nzm, criado com o GeoGebra
Agora responda:
a) Para [tex]a=180^\circ[/tex], o que ocorre com a figura?
b) E para [tex]a=360^\circ[/tex]?
Homotetia – Uma transformação não Isométrica
É uma transformação no plano onde as dimensões lineares não obrigatoriamente são preservadas. Para realizarmos uma Homotetia, precisamos de um centro [tex]O[/tex] e um número real e positivo [tex]k[/tex] denominado de razão. A Homotetia é uma aplicação que, a cada ponto [tex]P[/tex] de uma figura, faz corresponder o ponto [tex]P’[/tex] tal que [tex]\overline{OP’}=k \cdot \overline{OP}[/tex].
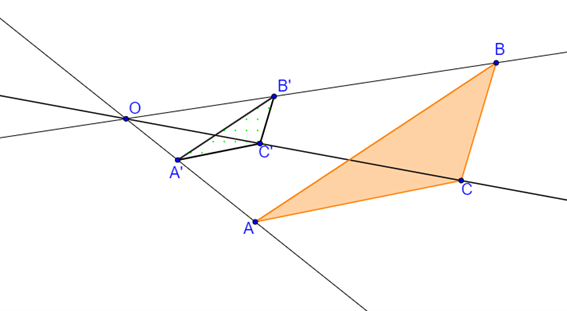
- O ponto [tex]O[/tex] é o centro da Homotetia;
- O número real e positivo [tex]k[/tex] é a razão de Homotetia;
- Se [tex]k \gt 1[/tex], a imagem é maior que o objeto e a Homotetia é uma ampliação. Veja o exemplo:
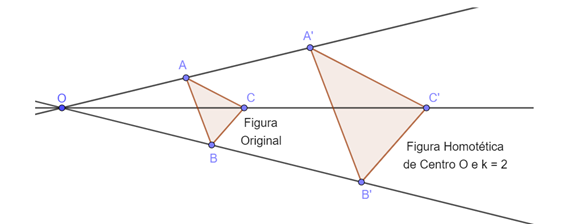
- Se [tex]k \lt 1[/tex], a imagem é menor que o objeto e a Homotetia é uma redução. Veja o exemplo:
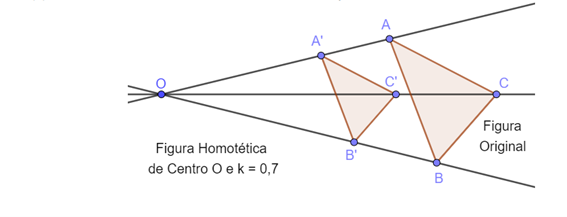
A Homotetia conserva a direção e o paralelismo dos segmentos que compõem a figura, bem como a amplitude e o sentido dos ângulos da mesma.
No applet a seguir, você pode escolher o número de lados do polígono no cursor e escolher a razão de semelhança que você deseja para a Homotetia.
1) Aguarde o aplicativo carregar completamente.
2) Escolha nos controles deslizantes o número [tex]n[/tex] de lados do polígono e a razão [tex]r[/tex] da homotetia de centro [tex]K[/tex].
3) Para reiniciar, clique nas setinhas que aparecem no canto superior direito do applet.
OBMEP_nzm, criado com o GeoGebra
Agora responda:
a) O que ocorre com a figura quando a razão é [tex]1[/tex]?
b) O que ocorre com a figura quando a razão é [tex]0,5[/tex]?
c) O que ocorre com a figura quando a razão é [tex]2[/tex]?

|
Finalizaremos esta Sala apresentando de forma intuitiva o conceito de Simetria. |
Simetria
Segundo o dicionário online de Português,
Assim, simetria é a harmonia de forma e tamanho entre as partes de um objeto ou imagem. Por exemplo, ao traçarmos uma linha reta dividindo ao meio uma figura, se ambas as metades, em relação a essa reta, coincidirem, dizemos que a figura é simétrica. Se uma forma apresenta o mesmo conjunto de pontos, apenas refletidos, em ambos os lados de uma reta, então dizemos que este objeto possui uma simetria axial.
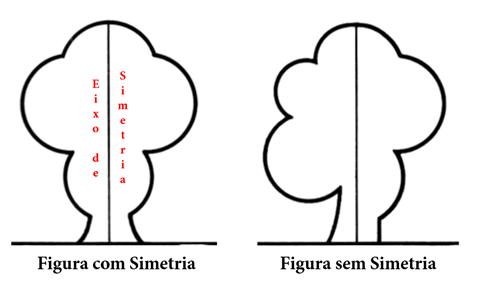
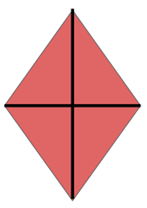
Uma figura pode possuir mais de um eixo de simetria. Por exemplo:
a) Figura com um eixo de simetria

b) Figura com dois eixos de simetria
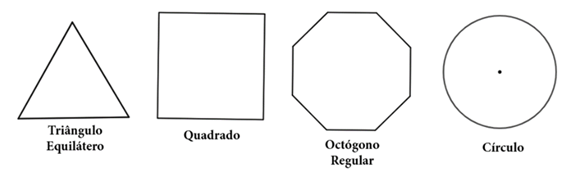
Agora responda:
Quantos eixos de simetria existem em cada figura abaixo?
A seguir, faremos um passeio por alguns tipos de simetria.
Axial, Reflexiva ou Bilateral
É aquela que se dá em relação à uma reta denominada Eixo de Simetria. Nela, a reta funciona como um espelho plano que reflete a imagem da figura original.
No applet a seguir, você verá como funciona a Simetria Axial.
Nelson Escalda, criado com o GeoGebra
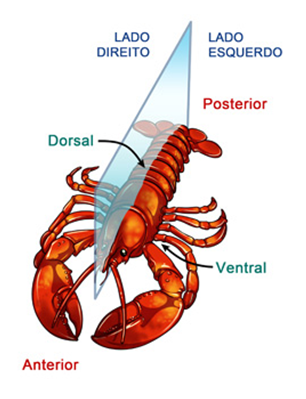
Esse tipo de simetria também é chamado de simetria reflexiva, ou simetria bilateral. Em três dimensões, esta simetria é aquela onde um plano corporal divide um corpo em imagens espelhadas ao longo de um eixo central. Nesse caso, temos um plano de simetria.
Central ou Pontual
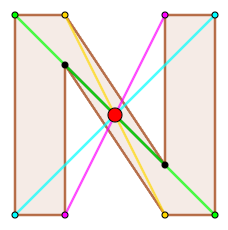
É aquela que se dá em relação a um ponto denominado Centro de Simetria. No plano, o ponto funciona como centro de rotação da figura em [tex]180^\circ[/tex].
Observe que a letra “de forma” N possui simetria pontual. Quais outras letras de forma do nosso alfabeto possuem este mesmo tipo de simetria?
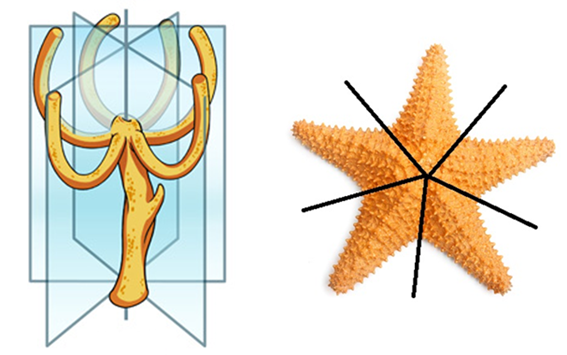
Radial
É aquela que possui um eixo passando através de uma forma, e suas partes se repetem em torno desse eixo. Em outras palavras, a forma fica dividida em partes iguais. Tal tipo de simetria é encontrada em algumas esponjas, em cnidários (como a anêmona-do-mar) e em equinodermos (como as estrelas-do-mar).

|
Observe a relação entre figuras simétricas e isometrias. Por exemplo, uma figura com simetria axial é uma figura invariante (que permanece a mesma) sob a isometria reflexão! Por outro lado, uma figura com simetria radial é invariante sob certas rotações. De modo simples e abrangente, dizemos que um objeto é simétrico se existe uma isometria que o leva em si mesmo. |

|
Esperamos que você tire proveito da explanação feita aqui. |
[1]SANTOMAURO, Beatriz. Geometria das Transformações. Nova Escola, 2011. Disponível em: https://novaescola.org.br/conteudo/2711/geometria-das-transformacoes. Acesso em: 15 de dezembro de 2021.
[2]Transformações geométricas nos Programas de Matemática do Ensino Básico e Secundário. Universidade de Coimbra. Disponível em: http://www.mat.uc.pt/~mat0829/Transformacoesgeometricas-2.pdf. Acesso em: 20 de dezembro de 2021.
[3]LIMA, Elon Lages. Isometrias. Coleção do Professor de Matemática. Rio de Janeiro, Sociedade Brasileira de Matemática (SBM), 1995.
[4]LIMA, Elon Lages., CARVALHO Paulo Cezar P. Coordenadas no Plano. 4ª Edição. Coleção do Professor de Matemática. Rio de Janeiro, Sociedade Brasileira de Matemática (SBM), 2002.
[5]ARAGÃO, Elaine Ramires. Transformações Geométricas Isometrias e Ornamentos. TCC (Curso de Especialização em Matemática) – Instituto de Matemática, Estatística e Computação Científica da Unicamp. Campinas, p. 34. 2011.
[6]O que é uma Reflexão Deslizante. Matemática em Casa. YouTube. Março de 2021. 1min 46s. Disponível em: https://www.youtube.com/watch?v=aGjwCNMIHxw&ab_channel=Matematicaemcasa. Acesso em 20 de dezembro de 2021.
[7]NETO, Jorge. Isometrias no plano – Reflexão axial. Disponível em: https://www.geogebra.org/m/T5d3y34T. Acesso em: 30 de dezembro de 2021.
[8]PISCARRETA, Sara Gabriela. Translação 8ºano parte 1. Disponível em: https://www.geogebra.org/m/xn9etjdc. Acesso em: 30 de dezembro de 2021.
[9]NETO, Jorge. Isometrias no Plano – Rotação. Disponível em: https://www.geogebra.org/m/bQmmKXyx. Acesso em: 30 de dezembro de 2021.
[10]ESCALDA, Nelson. Ampliação e Redução Usando o Método da Homotetia. Disponível em: https://www.geogebra.org/m/NnWGJd4d. Acesso em: 30 de dezembro de 2021.
[11]ESCALDA, Nelson. Simetria. Disponível em: https://www.geogebra.org/m/v7252gJc. Acesso em: 30 de dezembro de 2021.
[12]SILVA, Luiz Geraldo da. Simetria Axial, Rotacional e Central. Disponível em: https://www.geogebra.org/m/hZNcDFAv. Acesso em: 30 de dezembro de 2021.
[13]SILVA, Luiz Geraldo da. Motor de 4 tempos. Disponível em: https://www.geogebra.org/m/V8hdvXX7. Acesso em: 30 de dezembro de 2021.
