Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Muito Difícil)
(XXXII OPM – 2014) Em um quadrado [tex]ABCD[/tex], [tex] M[/tex] e [tex]N[/tex] são pontos dos lados [tex]\overline{AD}~ [/tex] e [tex]~\overline{CD}[/tex], respectivamente, tais que os ângulos [tex]B\hat{M}A[/tex] e [tex]N\hat{M}D[/tex] medem [tex]60^\circ.[/tex]
Calcule a medida do ângulo [tex]M\hat{B}N.[/tex]
Ajuda para a Solução 1
✐ Definição: Seja [tex]ACB[/tex] um triângulo retângulo com catetos e hipotenusa com comprimentos [tex]a,\, b,\, h[/tex], respectivamente. Seja [tex]\theta[/tex] a medida em graus de um dos ângulos agudos desse triângulo, [tex]0^{\circ} \lt\theta\lt 90^{\circ}[/tex].
Chamamos de cosseno de [tex]\theta[/tex], e denotamos por [tex]cos\, \theta[/tex], a razão entre os comprimentos do cateto adjacente a [tex]\theta[/tex] e da hipotenusa: [tex]\boxed{ cos\, \theta= \dfrac{b}{h}}.[/tex]
✐ No estudo da trigonometria, alguns ângulos são bastante utilizados e devido à frequência com que eles surgem em problemas e à importância que eles têm para a Geometria são denominados ângulos notáveis ou ângulos especiais ou, ainda, ângulos fundamentais. São eles os ângulos com medidas iguais a: [tex]30^\circ[/tex], [tex] 45^{\circ} [/tex] e [tex]60^\circ[/tex]. Os cossenos desses ângulos são:
[tex] \qquad \qquad cos\, 30^{\circ}=\dfrac{\sqrt{3}}{2}\quad ; \quad cos\, 45^{\circ}=\dfrac{\sqrt{2}}{2}\quad ;\quad cos\, 60^{\circ}=\dfrac{1}{2}[/tex].
✐ Se dois triângulos têm ordenadamente congruentes dois lados e o ângulo por eles definido, então estes triângulos são congruentes. pelo caso L.A.L.. (Se você não se lembra dos casos de congruência entre triângulos, clique AQUI.).
✐ A soma das medidas dos ângulos internos de um triângulo é [tex]180^\circ[/tex].
✐ Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e o seu comprimento por [tex]XY[/tex].
Solução 1
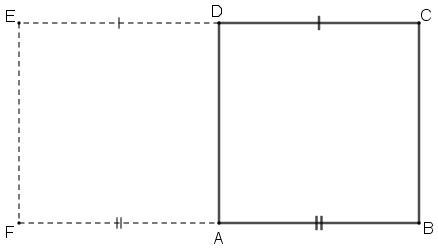
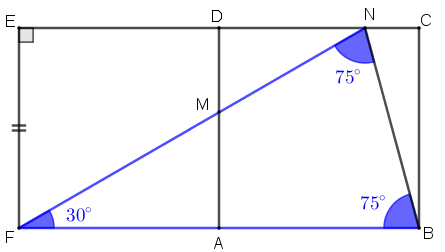
Prolonguemos os lados [tex]\overline{BA}[/tex] e [tex]\overline{CD}[/tex], de modo que [tex]D[/tex] e [tex]A[/tex] sejam os pontos médios dos segmentos prolongados [tex]\overline{EC}[/tex] e [tex]\overline{FB}[/tex], respectivamente, conforme ilustra a figura a seguir. Observe que, como [tex]ABCD[/tex] é um quadrado, então [tex]ADEF[/tex] também o é.
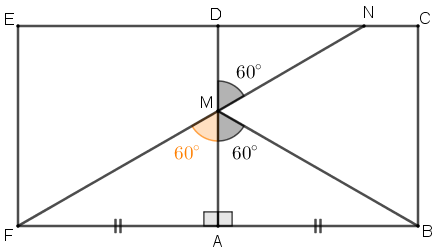
Como os triângulos [tex]ABM[/tex] e [tex] AFM[/tex] têm um ângulo reto, um lado comum e um lado com mesmo comprimento, eles são congruentes. Dessa forma, os ângulos [tex]B\hat MA[/tex] e [tex]A \hat M F[/tex] têm a mesma medida: [tex]60^\circ[/tex], e com isso, concluímos que nos pontos [tex]F,M[/tex] e [tex]N[/tex] são colineares.
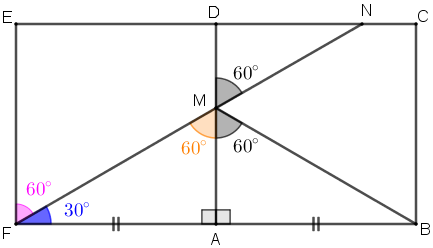
Com isso, a medida do ângulo [tex]M\hat F A[/tex] é [tex]180^\circ-90^\circ-60^\circ=30^\circ[/tex] e, consequentemente, a medida de [tex]E\hat F N[/tex] é:
[tex]\qquad \boxed{90^\circ-30^\circ=\color{#FF00FF}{60^\circ}}\,.[/tex]
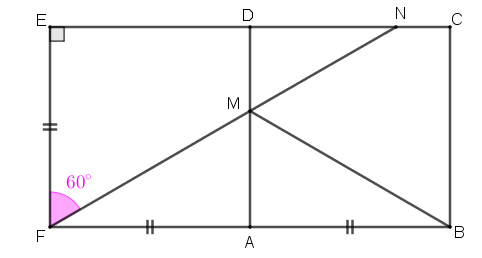
Observe o triângulo retângulo [tex]FEN[/tex] e veja que
[tex]\qquad \qquad cos\left(N\hat F E \right)=\dfrac{1}{2}=cos\, 60^\circ=\dfrac{EF}{FN}[/tex];
assim, segue que:
[tex]\qquad \qquad FN=2EF=2FA=FB.[/tex]
Dessa forma, concluímos que o triângulo [tex]FNB[/tex] é isósceles e, com isso obtemos que a medida do ângulo [tex]F\hat B N [/tex] é:
[tex]\qquad \boxed{\dfrac{180^\circ-30^\circ}{2}=\color{#0000FF}{75^\circ}\,} .[/tex]
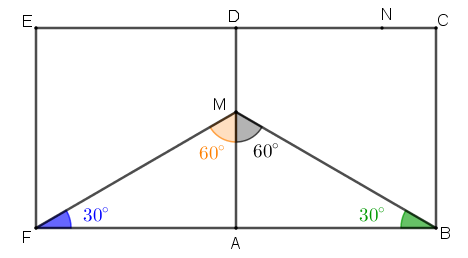
Por outro lado, observando o triângulo [tex]BMA[/tex], podemos concluir que a medida do ângulo [tex]FBM[/tex] é:
[tex]\qquad \boxed{180^\circ-30^\circ-\left(60^\circ+60^\circ\right)=\color{#009900}{30^\circ}\,} .[/tex]
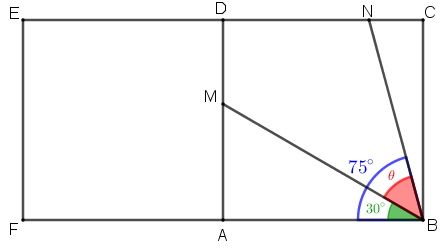
Finalmente, temos que a medida [tex]\textcolor{#FF0000}{\theta}[/tex], em graus, do ângulo [tex]M\hat{B}N[/tex] é dada por:
[tex]\qquad \qquad \textcolor{#FF0000}{\theta}=75^\circ-30^\circ = \fcolorbox{black}{#ffd3d3}{$45^\circ$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
Ajuda para a Solução 2
(1) Definição: Seja [tex]ACB[/tex] um triângulo retângulo com catetos e hipotenusa com comprimentos [tex]a,\, b,\, h[/tex], respectivamente. Seja [tex]\theta[/tex] a medida em graus de um dos ângulos agudos desse triângulo, [tex]0^{\circ} \lt\theta\lt 90^{\circ}[/tex].
Chamamos de tangente de [tex]\theta[/tex], e denotamos por [tex]tg\, \theta[/tex], a razão entre os comprimentos do cateto oposto e do cateto adjacente a [tex]\theta[/tex]: [tex]\boxed{ tg\, \theta= \dfrac{a}{b}}.[/tex]
(2) No estudo da trigonometria, alguns ângulos são bastante utilizados e devido à frequência com que eles surgem em problemas e à importância que eles têm para a Geometria são denominados ângulos especiais ou ângulos fundamentais. São eles os ângulos com medidas iguais a: [tex]30^\circ[/tex], [tex] 45^{\circ} [/tex] e [tex]60^\circ[/tex]. As tangentes desses ângulos são:
[tex]\qquad \qquad tg\, 30^{\circ}=\dfrac{\sqrt{3}}{3} \quad ; \quad tg\, 45^{\circ}=1\quad; \quad tg\, 60^{\circ}=\sqrt{3}[/tex]
e, em um triângulo retângulo, esses três ângulos são os únicos ângulos que possuem tais tangentes.
(3) A soma das medidas dos ângulos internos de um triângulo é [tex]180^\circ[/tex].
✐ Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e o seu comprimento por [tex]XY[/tex].
Solução 2
(Indicada a partir do 1º ano do E. M.)
Vamos fazer uma figura inicial contendo os dados do problema e as medidas dos ângulos [tex]A \hat B M[/tex], [tex]M \hat N D[/tex] e [tex]N \hat M B[/tex], obtidas utilizando a Ajuda (3) e o fato de os pontos [tex]A[/tex], [tex]M[/tex] e [tex]D[/tex] serem colineares. Na figura, denotamos as medidas em graus dos ângulos [tex]M \hat B N[/tex] e [tex]N \hat B C[/tex] por [tex]\theta[/tex] e [tex]\alpha[/tex], respectivamente.
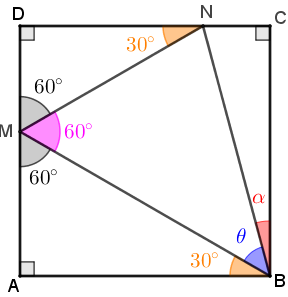
Agora, aplicando a definição dada na Ajuda (1) aos triângulos retângulos [tex]MAB[/tex], [tex]NDM[/tex] e [tex]BCN[/tex], utilizando a Ajuda (2) e denotando o comprimento dos lados do quadrado [tex]ABCD[/tex] por [tex]l[/tex] segue que:
| (a) [tex]\;\sqrt{3}=tg\, 60^\circ= \dfrac{AB}{MA}\\ \; MA=\dfrac{AB}{\sqrt{3}} \\ \; MA=\dfrac{l}{\sqrt{3}}. \qquad\textcolor{#800000}{(i)}[/tex] Assim, [tex]\; DA=DM+MA\\ \; DM=DA-MA\\ \; DM\stackrel{\textcolor{#800000}{(i)}}{=}l-\dfrac{l}{\sqrt{3}}.\quad\textcolor{#800000}{(ii)}[/tex] |
(b) [tex]\qquad \sqrt{3}=tg\, 60^\circ= \dfrac{DN}{DM}\\ \qquad DN=DM \cdot\sqrt{3}\,.\\ \,[/tex] Por [tex]\textcolor{#800000}{(ii)}[/tex], temos que: [tex]\; DN=\left(l-\dfrac{l}{\sqrt{3}}\right)\cdot\sqrt{3}\\ \; DN=\sqrt{3}\,\,l-l. \quad\textcolor{#800000}{(iii)}[/tex]
Dessa forma, |
(c) [tex]\; tg\, \alpha= \dfrac{NC}{CB}\\ \; tg\, \alpha\stackrel{\textcolor{#800000}{(iv)}}{=} \dfrac{2l-\sqrt{3}\,\,l}{l}\\ \; tg\, \alpha=2-\sqrt{3}. \quad\textcolor{#800000}{(v)} [/tex] |
Observe que
[tex]\qquad \alpha+\theta+30^\circ=90^\circ[/tex];
logo,
[tex]\qquad \alpha+\theta=60^\circ[/tex],
donde
[tex]\qquad tg\left(\alpha+\theta\right)=tg\, 60^\circ=\sqrt{3}[/tex].
Dessa forma, utilizando a fórmula da tangente da soma e a igualdade [tex]\textcolor{#800000}{(v)}[/tex], obtemos que:
[tex]\qquad tg\left(\alpha+\theta\right)=\sqrt{3}\\
\qquad \dfrac{tg\, \alpha+tg\, \theta}{1-tg\,\alpha \cdot tg\, \theta}=\sqrt{3}\\
\qquad \dfrac{\left(2-\sqrt{3}\right)+tg\, \theta}{1-\left(2-\sqrt{3}\right) \cdot tg\, \theta}\stackrel{\textcolor{#800000}{(v)}}{=}\sqrt{3}\\
\qquad 2-\sqrt{3}+tg\, \theta=\sqrt{3}\cdot\left(1-2\,tg\,\theta+\sqrt{3}\, tg\, \theta\right)\\
\qquad 2-\sqrt{3}+tg\, \theta=\sqrt{3}-2\sqrt{3}\,tg\,\theta+3\, tg\, \theta\\
\qquad 2-\sqrt{3}-\sqrt{3}=-2\sqrt{3}\,tg\,\theta+3\, tg\, \theta-tg\, \theta\\
\qquad 2-2\sqrt{3}=2\, tg\, \theta-2\sqrt{3}\,tg\,\theta\\
\qquad 2-2\sqrt{3}=tg\, \theta\cdot \left(2-2\sqrt{3}\right)\\
\qquad\cancel{ 2-2\sqrt{3}}=tg\, \theta\cdot \cancel{ \left(2-2\sqrt{3}\right)}\\
\qquad \boxed{tg\,\theta=1}\,.[/tex]
Assim, pela observação final da Ajuda (2), concluímos finalmente que a medida do ângulo [tex]M\hat{B}N[/tex] é [tex] \,\fcolorbox{black}{#ffd3d3}{$45^\circ$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
|
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |