Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Difícil)
A circunferência [tex]~\textcolor{red}{c}~[/tex] de centro [tex] \textcolor{red}{~O~}[/tex], que aparece na figura, é tangente às semirretas [tex] \textcolor{#0099FF}{PX}[/tex] e [tex] \textcolor{#0099FF}{PY}[/tex] nos pontos [tex] A[/tex] e [tex] B[/tex], respectivamente.
- Afirmação: O centro [tex] \textcolor{red}{~O~}[/tex] pertence à bissetriz interna do ângulo [tex] \textcolor{#0099FF}{X\hat{P}Y}.[/tex]
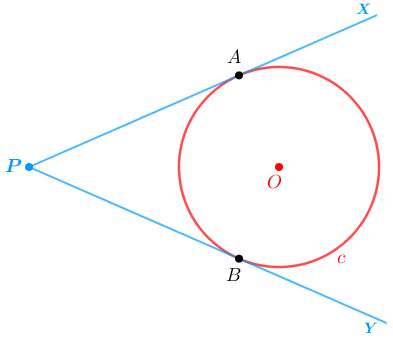
Essa afirmação é verdadeira? Justifique sua resposta.

Lembretes:
(1) Toda tangente a uma circunferência é perpendicular ao raio no ponto de tangência.
(2) Congruência de triângulos retângulos: Se dois triângulos retângulos têm ordenadamente congruentes um cateto e a hipotenusa, então estes triângulos são congruentes.
✐ Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]E[/tex] e [tex]F[/tex], por [tex]\overline {EF} [/tex] e o seu comprimento por [tex]EF.[/tex]
Solução
A partir dos dados do problema, devemos garantir que a semirreta [tex]PO[/tex] é a bissetriz do ângulo [tex] \textcolor{#0099FF}{X\hat{P}Y}.[/tex]
Para isso, inicialmente vamos traçar os segmentos [tex]\overline {OA}\, [/tex] e [tex]\, \overline {OB}.[/tex]
De acordo com o Lembrete (1) , definimos dois triângulos retângulos: o triângulo [tex]PAO[/tex] e o triângulo [tex]PBO.[/tex]
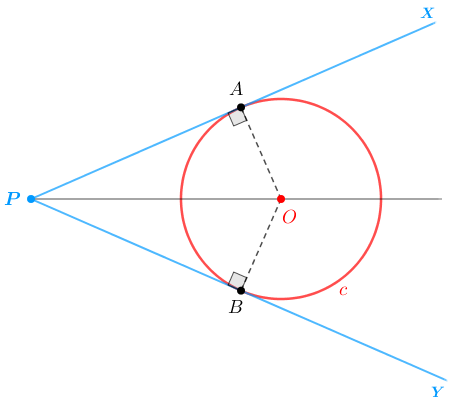
Observe que os segmentos [tex]\overline {OA}\, [/tex] e [tex]\, \overline {OB}[/tex] são raios de [tex]~\textcolor{red}{c}~[/tex] e, portanto, são congruentes. Assim, pelo Lembrete (2), os triângulos [tex]PAO[/tex] e [tex]PBO[/tex] são congruentes.
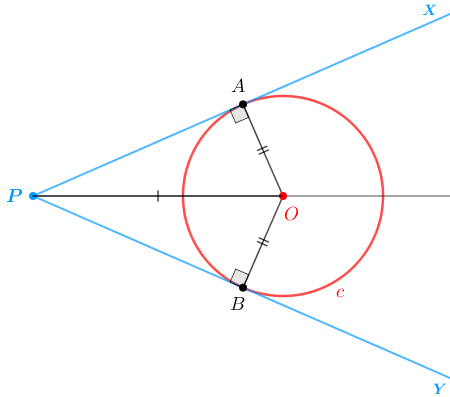
Com isso, particularmente, os ângulos [tex]\textcolor{#FF33CC}{A\hat{P}O}[/tex] e [tex]\textcolor{#006400}{B\hat{P}O}[/tex] têm a mesma medida e, portanto, a semirreta [tex]PO[/tex] é a bissetriz interna do triângulo [tex] \textcolor{#0099FF}{X\hat{P}Y}.[/tex]
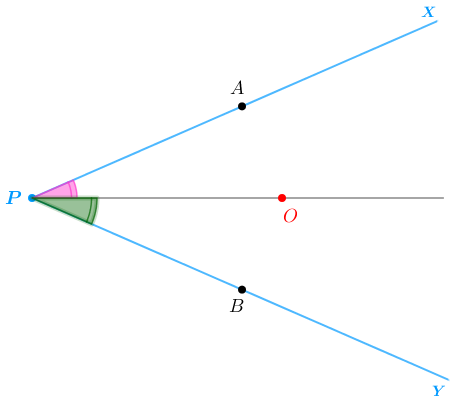
Logo, o centro [tex] \textcolor{red}{~O~}[/tex] pertence à bissetriz interna do ângulo [tex] \textcolor{#0099FF}{X\hat{P}Y}[/tex] e a afirmação é verdadeira.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
