Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Difícil)
(VIII ONEM, 2011 – Adaptado) Vejam que propriedade interessante o número [tex]1037[/tex] tem:
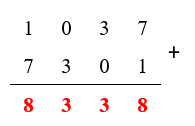
Perceberam?
A soma de [tex]1037[/tex] com [tex]7301[/tex] é um palíndromo (ou capicua), isto é, um número que permanece o mesmo quando lemos os seus dígitos de “frente para trás” ou de “trás para frente”.
Por esse motivo, [tex]1037[/tex] é dito um número versátil, de acordo com a seguinte definição:
Quantos números versáteis de quatro dígitos existem?
Lembrete:
 ✏ Princípio Fundamental da Contagem, ou Princípio Multiplicativo (para duas decisões) :
✏ Princípio Fundamental da Contagem, ou Princípio Multiplicativo (para duas decisões) :
Se uma decisão A pode ser tomada de [tex] m [/tex] maneiras distintas e, tomada essa decisão A, uma decisão B puder ser tomada de [tex] n [/tex] maneiras distintas, então a quantidade de maneiras de se tomar sucessivamente as decisões A e B é igual a [tex]~\boxed{ m \times n}\, . [/tex]
(Se você não se lembra desse Princípio, seria interessante dar uma passadinha nesta Sala de Estudo.)
Solução
Seja [tex]abcd[/tex] um número versátil. (Antes de prosseguir, observe que aqui a notação [tex]abcd[/tex] não indica um produto e sim a representação de um número de quatro algarismos no sistema decimal.)
Assim, segundo a definição dada no problema, [tex]P=abcd+dcba[/tex] é um palíndromo com quatro algarismos.
Vamos observar os algarismos de milhar, centena, dezena e unidade da soma [tex]P=abcd+dcba[/tex] utilizando o esqueminha da adição.
[tex]\begin{array}{c c c c}
\textcolor{red}{Mi}&\textcolor{red}{Ce}&\textcolor{red}{De}&\textcolor{red}{Un}\\
\,a&b&c&d\,\\
\,d&c&b&a\,\\
\hline
\end{array}\,+[/tex]
- Como [tex]P[/tex] tem quatro algarismos, a soma [tex]a+d[/tex] que define o algarismo dos milhares de [tex]P[/tex] não pode ser maior do que [tex]9[/tex], ou seja, [tex]\boxed{a+d \leqslant 9}\,.[/tex] Como [tex]P[/tex] é palíndromo seu algarismo das unidades é também [tex]a+d.[/tex]
- Como o algarismo dos milhares é exatamente [tex]a+d[/tex], então, na definição do algarismo das centenas da soma [tex]abcd+dcba[/tex], a soma [tex]b+c[/tex] não leva uma unidade de milhar para a soma [tex]a+d[/tex]. Dessa forma, [tex]\boxed{b+c \leqslant 9}\,.[/tex] Como [tex]P[/tex] é palíndromo, seu algarismo das dezenas é também [tex]b+c.[/tex]
[tex]\begin{array}{c c c c}
\textcolor{red}{Mi}&\textcolor{red}{Ce}&\textcolor{red}{De}&\textcolor{red}{Un}\\
\,a&b&c&d\,\\
\,d&c&b&a\,\\
\hline
\,\,a+d\,&\,b+c\,&\,b+c\,&\,a+d\,\,\\
\end{array}+[/tex]
Pronto, com as informações de que [tex]\,\boxed{a+d \leqslant 9}\,[/tex] e [tex]\,\boxed{b+c \leqslant 9}\,[/tex] já podemos contar quantos números versáteis existem.
Vamos lá!
-
[tex]\textcolor{#800000}{(1)}[/tex] Para contar a quantidade de algarismos [tex]a[/tex] e [tex]d[/tex], além da informação que [tex]a+d \leqslant 9 [/tex], observe que o número [tex]abcd[/tex] tem quatro dígitos e não é um múltiplo de [tex]10[/tex]. Com isso, temos três condições: [tex]\boxed{a+d \leqslant 9}[/tex], [tex]\, \boxed{1\leqslant a}\,[/tex] e [tex]\, \boxed{1\leqslant d}\,[/tex].
- Para [tex]a=1[/tex], temos [tex]8[/tex] possibilidades para [tex]d[/tex];
- para [tex]a=2[/tex], temos [tex]7[/tex] possibilidades para [tex]d[/tex];
- para [tex]a=3[/tex], temos [tex]6[/tex] possibilidades para [tex]d[/tex];
- para [tex]a=4[/tex], temos [tex]5[/tex] possibilidades para [tex]d[/tex];
- para [tex]a=5[/tex], temos [tex]4[/tex] possibilidades para [tex]d[/tex];
- para [tex]a=6[/tex], temos [tex]3[/tex] possibilidades para [tex]d[/tex];
- para [tex]a=7[/tex], temos [tex]2[/tex] possibilidades para [tex]d[/tex];
- para [tex]a=8[/tex], temos [tex]1[/tex] possibilidade para [tex]d[/tex];
- não podemos ter [tex]a=9[/tex], pois, nesse caso, teríamos [tex]d=0[/tex].
- para [tex]b=0[/tex], temos [tex]10[/tex] possibilidades para [tex]c[/tex];
- para [tex]b=1[/tex], temos [tex]9[/tex] possibilidades para [tex]c[/tex];
- para [tex]b=2[/tex], temos [tex]8[/tex] possibilidades para [tex]c[/tex];
- para [tex]b=3[/tex], temos [tex]7[/tex] possibilidades para [tex]c[/tex];
- para [tex]b=4[/tex], temos [tex]6[/tex] possibilidades para [tex]c[/tex];
- para [tex]b=5[/tex], temos [tex]5[/tex] possibilidades para [tex]c[/tex];
- para [tex]b=6[/tex], temos [tex]4[/tex] possibilidades para [tex]c[/tex];
- para [tex]b=7[/tex], temos [tex]3[/tex] possibilidades para [tex]c[/tex];
- para [tex]b=8[/tex], temos [tex]2[/tex] possibilidades para [tex]c[/tex];
- para [tex]b=9[/tex], temos [tex]1[/tex] possibilidade para [tex]c[/tex].
Assim, temos [tex]8+7+6+5+4+3+2+1=36[/tex] possibilidades para escolha simultânea de [tex]a[/tex] e [tex]d.[/tex]
[tex]\,\,\,\,[/tex]
[tex]\textcolor{#800000}{(2)}[/tex] Para contar a quantidade de algarismos [tex]b[/tex] e [tex]c[/tex], além da informação de que [tex]\,\boxed{0 \leqslant b,c \leqslant 9}[/tex], utilizaremos a informação [tex]\boxed{b+c \leqslant 9}.[/tex]
Logo, temos [tex]10+9+8+7+6+5+4+3+2+1=55[/tex] possibilidades para escolha simultânea de [tex]b[/tex] e [tex]c.[/tex]
Finalmente, pelo Princípio Fundamental da Contagem, existem [tex] \, \fcolorbox{black}{#eee0e5}{$36 \times 55=1\,980$}[/tex] números versáteis de quatro dígitos/algarismos.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
