(A) Problema para ajudar na escola: Dois polígonos

Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Fácil)

(ONEM – 2010) Os dois polígonos mostrados na figura são regulares, têm um lado em comum e são coplanares.

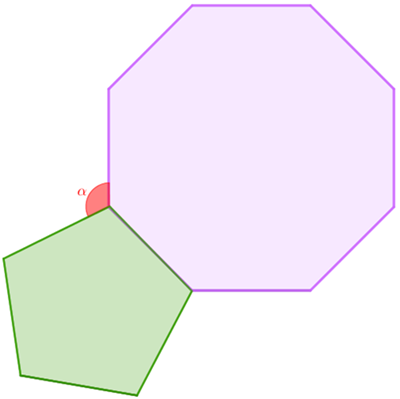
Determinar a medida angular [tex]\textcolor{red}{\alpha}[/tex], em graus.

Solução

Observe que se conseguirmos obter as medidas angulares [tex]\textcolor{#CC66FF}{\theta}[/tex] e [tex]\textcolor{#339900}{\beta}[/tex] indicadas na figura abaixo, facilmente obtemos a medida [tex]\textcolor{red}{\alpha}[/tex], uma vez que [tex]\boxed{\textcolor{red}{\alpha}+\textcolor{#339900}{\beta}+\textcolor{#CC66FF}{\theta}=360^\circ}.[/tex]
Vamos fazê-lo por etapas.

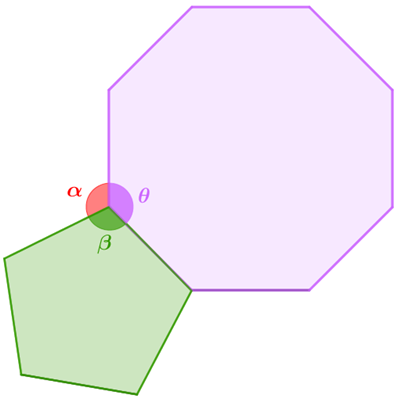
• O polígono colorido de verde é um pentágono.
  Pela fórmula citada no Lembrete, a soma dos ângulos internos de um pentágono é
  [tex]\qquad \qquad S_5=\left(5-2\right)\cdot 180^\circ=540^\circ.[/tex]
  Como o pentágono da figura é regular, particularmente todos os seus ângulos internos têm a mesma medida, portanto:
  [tex]\qquad \qquad \textcolor{#339900}{\beta=\dfrac{540^\circ}{5}}[/tex]

[tex]\qquad \qquad \textcolor{#339900}{\boxed{\beta=108^\circ}}.[/tex]

• O polígono colorido de lilás é um octógono.
  Pela fórmula citada no Lembrete, a soma dos ângulos internos de um octógono é
  [tex]\qquad \qquad S_8=\left(8-2\right)\cdot 180^\circ=1080^\circ.[/tex]
  Como o octógono da figura é regular, também todos os seus ângulos internos têm a mesma medida, logo:
  [tex]\qquad \qquad \textcolor{#CC66FF}{\theta=\dfrac{1080^\circ}{8}}[/tex]

[tex]\qquad \qquad \textcolor{#CC66FF}{\boxed{\theta=135^\circ}}.[/tex]

A partir dessas duas medidas, podemos concluir que:
[tex]\qquad \qquad \textcolor{red}{\alpha}=360^\circ-\textcolor{#339900}{\beta}-\textcolor{#CC66FF}{\theta}[/tex]
[tex]\qquad \qquad \textcolor{red}{\alpha}=360^\circ-\textcolor{#339900}{108^\circ}-\textcolor{#CC66FF}{135^\circ}[/tex]
[tex]\qquad \qquad \textcolor{red}{\boxed{\alpha=117^\circ}}[/tex].

Solução elaborada pelos Moderadores do Blog.