Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Médio)
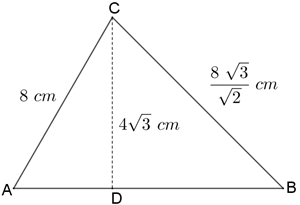
Determine as medidas dos segmentos [tex]\overline{BC}\, [/tex] e [tex]\, \overline{AB}[/tex] mostrados na figura abaixo.
O triângulo [tex]ABC[/tex] é retângulo?
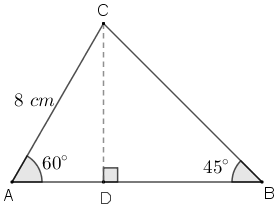
Figura não proporcional aos dados do problema.
Ajuda
✐ Definição: Seja [tex]ACB[/tex] um triângulo retângulo com catetos e hipotenusa com comprimentos [tex]a,\, b,\, h[/tex], respectivamente. Seja [tex]\theta[/tex] a medida em graus de um dos ângulos agudos desse triângulo, [tex]0^{\circ} \lt\theta\lt 90^{\circ}[/tex].
Chamamos de cosseno de [tex]\theta[/tex], e denotamos por [tex]cos\, \theta[/tex], a razão entre os comprimentos do cateto adjacente a [tex]\theta[/tex] e da hipotenusa:[tex]\boxed{ cos\, \theta= \dfrac{b}{h}}.[/tex]
Chamamos de seno de [tex]\theta[/tex], e denotamos por [tex]sen\, \theta[/tex], a razão entre os comprimentos do cateto oposto a [tex]\theta[/tex] e da hipotenusa:[tex]\boxed{ sen\, \theta= \dfrac{a}{h}}.[/tex]
✐ No estudo da trigonometria, alguns ângulos são bastante utilizados e devido à frequência com que eles surgem em problemas e à importância que eles têm para a Geometria são denominados ângulos especiais ou ângulos fundamentais. São eles os ângulos com medidas iguais a: [tex]30^\circ[/tex], [tex] 45^{\circ} [/tex] e [tex]60^\circ[/tex].
Os senos e cossenos desses ângulos são:
a) [tex]\, \, sen\, 30^{\circ}=\dfrac{1}{2}\qquad\qquad\, \, \, \, cos\, 30^{\circ}=\dfrac{\sqrt{3}}{2}[/tex] .
b) [tex]\, \, sen\, 45^{\circ}=\dfrac{\sqrt{2}}{2}\qquad\qquad[/tex] [tex] cos\, 45^{\circ}=\dfrac{\sqrt{2}}{2}[/tex].
c) [tex]\, \, sen\, 60^{\circ}=\dfrac{\sqrt{3}}{2}\qquad\qquad[/tex] [tex] cos\, 60^{\circ}=\dfrac{1}{2}[/tex] .
✐ Teorema de Pitágoras: Em um triângulo retângulo, o quadrado da hipotenusa é a soma dos quadrados dos catetos.
✐ A soma das medidas dos ângulos internos de um triângulo é [tex]180^\circ[/tex].
✐ Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e o seu comprimento por [tex]XY[/tex].
Solução
Dos três triângulos que aparecem na figura do problema conhecemos apenas a medida do comprimento de um dos lados; precisamos obter medidas relativas a outros lados desses triângulos.
Como para o triângulo [tex]BCD[/tex] não temos medidas de lados definidas, vamos iniciar por ele. Esse triângulo tem um lado comum com o triângulo [tex]CAD[/tex] e é um triângulo retângulo; dessa forma, vamos utilizar a relação entre cateto oposto e hipotenusa e a tabelinha com os senos, cossenos e tangentes dos ângulos especiais para obter, então, o comprimento do lado [tex]\overline{CD}:[/tex]
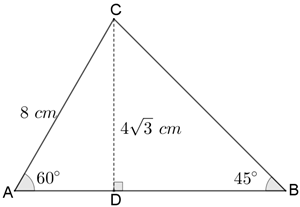[tex]\qquad sen\, 60^\circ= \dfrac{CD}{8}\\
\qquad \dfrac{\sqrt{3}}{2}= \dfrac{CD}{8}\\
\qquad CD= 8 \times \dfrac{\sqrt{3}}{2}\\
\qquad \boxed{CD= 4\, \sqrt{3}\, \text{cm}}.[/tex]
Agora já podemos determinar a medida do lado [tex]\overline{BC}:[/tex]
[tex]\qquad sen\, 45^\circ= \dfrac{ 4\, \sqrt{3}}{BC}\\
\qquad \dfrac{\sqrt{2}}{2}= \dfrac{ 4\, \sqrt{3}}{BC}\\
\qquad BC= \left(4\, \sqrt{3}\right)\times \dfrac{2}{\sqrt{2}}\\
\qquad \, \fcolorbox{black}{#eee0e5}{$BC= \dfrac{8\, \sqrt{3}}{\sqrt{2}}\, \text{cm}$}\, .[/tex]
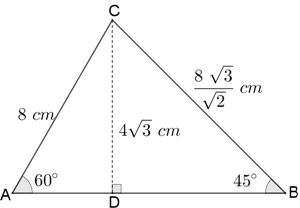
Agora, resista à tentação de aplicar o Teorema de Pitágoras ao triângulo [tex]ABC[/tex] para obter a medida do lado [tex]\overline{AB}[/tex]!
Já respondendo a pergunta formulada no problema, o triângulo [tex]ABC[/tex] não é um triângulo retângulo.
- Com efeito, como a soma das medidas dos ângulos internos de um triângulo é [tex]180^\circ[/tex], a medida do terceiro lado do triângulo é [tex]180^\circ – \left(60^\circ+45^\circ\right)=75^\circ[/tex] e, dessa forma o triângulo [tex]ABC[/tex] não tem um ângulo reto.
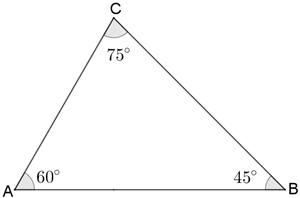
Vamos então determinar a medida do lado [tex]\overline{AB}[/tex] aplicando o teorema de Pitágoras aos triângulos retângulos [tex]ADC[/tex] e [tex]CDB[/tex] para obter as medidas dos lados [tex]\overline{AD}[/tex] e [tex]\overline{DB}.[/tex]
|
[tex]\qquad \qquad \Delta ADC:[/tex] [tex]\qquad 8^2=AD^2+\left(4\sqrt{3}\right)^2\\ \qquad AD^2=64-48\\ \qquad AD^2=16\\ \qquad AD=\pm 4.\\[/tex] Como [tex]AD \gt 0[/tex], [tex]\boxed{AD=4\, \text{cm}}.[/tex] |
[tex]\qquad \qquad \Delta CDB:[/tex] [tex]\qquad \left(\dfrac{8\, \sqrt{3}}{\sqrt{2}}\right)^2=BD^2+\left(4\sqrt{3}\right)^2\\ \qquad BD^2=96-48\\ \qquad BD^2=48\\ \qquad BD=\pm 4\sqrt{3}.\\[/tex] Como [tex]BD\gt 0[/tex], [tex]\boxed{BD=4\sqrt{3}\, \text{cm}}.[/tex] |
Poderíamos também ter obtido as medidas dos lados [tex]\overline{AD}[/tex] e [tex]\overline{DB}[/tex] utilizando a fórmula do cosseno apresentada na ajuda.
| [tex]\qquad cos\, 60^\circ= \dfrac{AD}{8}\\ \qquad \dfrac{1}{2}= \dfrac{AD}{8}\\ \qquad AD= \dfrac{8}{2}\\ \qquad \boxed{AD= 4\, \text{cm}}.[/tex] |
[tex]\qquad cos\, 45^\circ= \dfrac{BD}{\dfrac{8\, \sqrt{3}}{\sqrt{2}}}\\ \qquad \dfrac{\sqrt{2}}{2}= \dfrac{BD}{\dfrac{8\, \sqrt{3}}{\sqrt{2}}}\\ \qquad BD= \dfrac{\sqrt{2}}{2} \times \dfrac{8\, \sqrt{3}}{\sqrt{2}}\\ \qquad \boxed{BD= 4\sqrt{3}\, \text{cm}}.[/tex] |
Particularmente, poderíamos ter obtido a medida do lado [tex]\overline{DB}[/tex] observando que o triângulo [tex]CDB[/tex] é isósceles.
Finalizando, como [tex]\overline{AB}=\overline{AD}+\overline{DB}[/tex], temos que [tex]AB= (4+4\sqrt{3})\, \text{cm}[/tex], ou ainda, [tex]\, \fcolorbox{black}{#eee0e5}{$AB= 4\left(1+\sqrt{3}\right)\, \text{cm}$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
|
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |