Sala 2 – Mãos na massa com a NASA
Aos 5 anos de idade, um garoto brasileiro chamado Miro Latansio Tsai se tornou a pessoa mais jovem do mundo a identificar um asteroide. Até fevereiro de 2022, ele tinha descoberto, no total, 15 corpos celestes confirmados pela Nasa (Agência Espacial Norte-Americana).

Fonte: https://diariodonordeste.verdesmares.com.br/ultima-hora/ciencia/aos-5-anos-crianca-brasileira-se-torna-pessoa-mais-jovem-a-descobrir-asteroide-no-mundo-1.3189633. Acesso em: jun 2024.
Mas o que esta linda notícia tem a ver com a Matemática? Muita coisa. Nas palavras do grande cientista e matemática Galileu Galilei,
Tanto é que a NASA tem investido na formação matemática de jovens e crianças do mundo inteiro. De fato, desde 2004, a NASA possui um Space Math@ (Espaço da Matemática), na qual desenvolve problemas de matemática projetados para mostrar como as descobertas da NASA na Terra e na ciência espacial são conectadas a uma variedade de tópicos e habilidades matemáticas. Em 2011, mais de 400 desses problemas estavam disponíveis online, ou poderiam ser encontrados em uma série de livros de tópicos especiais (Matemática do Buraco Negro, Matemática da Terra etc.). E o projeto não para de crescer. Frequentemente, os comunicados de imprensa da NASA servem como ‘gancho’ para fornecer um tópico adequado a partir do qual um problema matemático apropriado é desenvolvido. Em um exemplo, os alunos puderam ler um comunicado de imprensa anunciando a descoberta de um novo planeta e calcular, a partir dois pontos em sua órbita elíptica, a equação da órbita, seu semieixo maior e o período orbital do planeta. Outro exemplo é a série “Pi in the sky”, uma série de desafios matemáticos reais que utilizam o [tex]\pi[/tex] para sua resolução (confira um deles no nosso Blog). Assim, o Space Math usa as últimas descobertas das missões de ciência espacial da NASA para desenvolver problemas de matemática apropriados para séries escolares, abrangendo todas as áreas de matemática contemporânea na educação formal.
As relações não param por aí! Até a OBMEP faz parte da interação entre a NASA e a matemática. Bolsas de estudo, cursos na NASA e a participação na Olimpíada Europeia Feminina de Matemática (EGMO, na sigla em inglês) estão entre as oportunidades surgidas para algumas estudantes que se destacaram na OBMEP. Viagens à NASA também são prêmios de outras olimpíadas, como a olimpíada carioca de matemática.
Seja olhando as estrelas à noite ou tornando-se um pesquisador do espaço, como a ex-medalhista Katarine Klitzke, vocês com certeza vão perceber cada vez mais que o espaço é repleto de matemática. Convidamos vocês a realizarem as seguintes atividades, aplicações das equações quadráticas, e, de quebra, realizarem uma mostra para sua escola, ilustrando a matemática do espaço, ou o espaço da matemática.
Vamos?!
Atividade 1 – Supernova
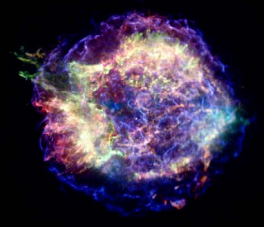
A concha de supernova Cass-A em expansão, vista pelo Observatório de Raios-X Chandra (Cortesia: NASA/Chandra)
Quando uma estrela gigante chega ao fim de sua vida, produz-se uma explosão a que se dá o nome de supernova. Quando uma estrela explode como uma supernova, uma onda de choque viaja desde o centro da explosão ao espaço interestelar. Como a casca de detritos expande, ela comprime o gás interestelar ao seu redor para uma densidade mais alta.
A quantidade de compressão pode ser modelada pela fórmula
[tex]y(x)=0,67x^2+6x−2,66,[/tex]
onde [tex]x[/tex] é a razão entre a densidade do gás adiante da frente de choque e a densidade atrás da frente de choque.
(1) Use a fórmula resolutiva para encontrar as duas raízes de [tex]y[/tex].
(2) Qual é a localização do vértice de [tex]y[/tex]?
(3) Esboce o gráfico de [tex]y[/tex].
(4) Somente escolhas para [tex]x[/tex] que sejam positivas definidas sobre o conjunto de números reais são soluções permitidas para [tex]y[/tex]. Qual raiz de [tex]y[/tex] é uma solução permitida?
(5) O valor de [tex]x[/tex] que satisfaz [tex]y(x)=0[/tex] dá a razão entre a densidade do gás por trás da onda de choque e a densidade do meio interestelar não perturbado. Por qual fator o meio interestelar foi comprimido ao passar pela onda de choque?
Nota: A fórmula para [tex]y(x)[/tex] foi derivada pelos astrônomos Shull e Draine, no livro ‘Interstellar Processes’ página 288-289, e representa a quantidade de entropia (desordem) criada pela frente de choque. As raízes da equação representam compressões para as quais a mudança de entropia é zero.
Atividade 2 – Medindo asteroides

Ganimedes passando atrás de Júpiter durante uma ocultação: 9 de abril de 2007 (NASA/Hubble)
Embora os eclipses solares totais sejam “dramáticos”, os astrônomos usam outro fenômeno relacionado para determinar o tamanho e a forma de asteroides distantes: eles observam os asteroides enquanto eles bloqueiam as estrelas atrás deles – essas ocultações revelam a forma e o tamanho dos asteroides enquanto suas “sombras” varrem a Terra. Quando um asteroide passa na frente de uma estrela durante uma ocultação, os astrônomos podem medir com precisão quando a estrela desaparece e clareia à medida que o asteroide passa. Observadores na superfície da Terra verão essa ocultação em diferentes orientações e, combinando seus dados de tempo, a forma do asteroide pode ser encontrada. A fórmula abaixo mostra a trilha de ocultação de uma estrela hipotética à medida que a Lua passa:
[tex]D^2(t)=225t^2–3825t+16545.[/tex]
Nesta fórmula, [tex]t[/tex] é o tempo em minutos e [tex]D(t)[/tex] é a distância entre o centro da Lua e o centro da estrela que passa, em minutos de arco. Ou seja, é a distância angular, do ponto de vista do observador. Nos problemas a seguir adote a definição de que [tex]y(t)=D^2(t)[/tex], para simplificar a forma da equação.
(1) Use a fórmula de resolução da equação quadrática para mostrar que, para a ocultação desta estrela em particular, nunca ocorre [tex]y(t)=0[/tex].
(2) Em que instante [tex]t[/tex] a estrela atingirá a distância mais próxima do centro da Lua?
(3) Qual será a distância, em minutos de arco, entre a estrela e o centro da Lua na sua maior aproximação?
OBS.: Minuto, minuto de arco ou arco-minuto, usualmente abreviado como arcmin ou amin, é uma unidade de medida angular equivalente a [tex]1/60[/tex] de grau. Trata-se de uma unidade de medida usada em astronomia e geometria.
(4) Se o raio da Lua for de [tex]15[/tex] minutos de arco, a que distância da borda da Lua a estrela passará na sua maior aproximação?
(5) Faça um gráfico da função [tex]y[/tex]. Em que instantes a estrela estará a [tex]41[/tex] minutos de arco do centro da Lua?
Atividade 3 – Modelagem da curva de Keeling
A variação anual do dióxido de carbono na atmosfera, mostrada na ‘Curva de Keeling’ abaixo, é motivo de grande preocupação, pois contribui para o aquecimento global e as mudanças climáticas.
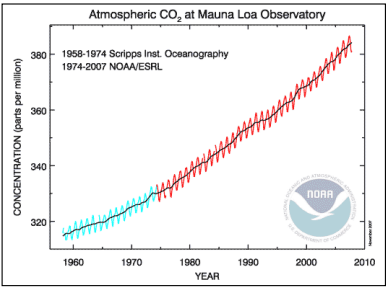
Os dados para o aumento do dióxido de carbono desde 1960 são mostrados na tabela abaixo.

O ‘Ano’ (Year) é o número de anos desde 1960 e ‘CO2’ é a concentração de dióxido de carbono na atmosfera em partes por milhão (PPM).
(1) Uma porção da Curva de Keeling pode ser modelada por uma equação parabólica na forma
[tex]CO_2(t)=at^2+bt+c,[/tex]
onde [tex]t[/tex] é o número de anos a partir de 1960. Usando três pontos de dados na tabela, resolva um conjunto de três equações lineares simultâneas para determinar a equação quadrática mais adequada para esses dados atmosféricos.
(2) Faça um gráfico dos dados e da equação quadrática mais adequada para o período de 1960 a 2100 em intervalos de décadas.
(3) Qual é a sua previsão para o ano de 2050? E para o ano 2100?
Atividade Final
Convidamos vocês a realizarem uma mostra na sua escola com o tema
“Aplicações da matemática à astronomia: resolvendo problemas reais”

Vocês podem inserir outras informações e pesquisarem mais problemas no Space Math @, com a ajuda de seus professores de inglês e de matemática. A história de Katherine Johnson com certeza servirá de inspiração!
Enviem para o nosso e-mail registros da mostra, e poderemos divulgar no nosso site!
Bons estudos!
Caso queira voltar para a primeira Sala, é só clicar no botão abaixo:
| Sala 1 |
