Problema
(Indicado a partir do 2º ano do E. M.)
Considere os seguintes cenários:
“Uma pessoa tem dois filhos. Sabe-se que pelo menos um deles é menino”.
“Uma pessoa tem dois filhos. Sabe-se que o mais velho é um menino”.
Calcule, em cada cenário, a probabilidade dessa pessoa ter dois meninos.
Extraído de Prakash Gorroochurn. Classic Problems of Probability.

Lembrete
Considere um experimento aleatório com espaço amostral [tex]\Omega[/tex] no qual está definida uma função probabilidade [tex]P[/tex].
Dados dois eventos [tex]A[/tex] e [tex]B[/tex] de [tex]\Omega[/tex], com [tex]P(B)\ne 0[/tex], a probabilidade condicional de [tex]A[/tex] na certeza de [tex]B[/tex] é a razão
[tex]\qquad \qquad P(A|B)=\dfrac{P(A\cap B)}{P(B)}\,.[/tex]
Solução
Para resolver essa questão vamos usar o conceito de probabilidade condicional e a probabilidade da união de eventos.
Consideremos [tex]A[/tex] o evento “o filho mais jovem é um menino” e [tex]B[/tex] o evento “o filho mais velho é um menino”. Observe que [tex]P(A)=\dfrac{1}{2}[/tex] e [tex]P(B)=\dfrac{1}{2}[/tex]. Como os eventos [tex]A[/tex] e [tex]B[/tex] são independentes, temos [tex]P(A\cap B)=P(A)\times P(B)=\dfrac{1}{4}.[/tex]
Na primeira situação, estamos interessados em calcular a probabilidade do evento [tex]A \cap B[/tex] dado que ocorre o evento [tex]A \cup B[/tex]. Assim,
[tex]\qquad P(A\cap B | A \cup B)=\dfrac{P((A\cap B) \cap ( A \cup B))}{P(A\cup B)}=\dfrac{P(A\cap B)}{P(A)+P(B)-P(A\cap B)}=\dfrac{\dfrac{1}{4}}{\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{4}}=\dfrac{1}{3}.[/tex]
Na segunda situação estamos interessados em calcular a probabilidade do evento [tex]A \cap B[/tex] dado que ocorre o evento [tex] B[/tex]. Assim,
[tex]\qquad P(A\cap B | B)=\dfrac{P((A\cap B) \cap B))}{P( B)}=\dfrac{P(A\cap B)}{P(B)}=\dfrac{\dfrac{1}{4}}{\dfrac{1}{2}}=\dfrac{1}{2}.[/tex]
A diferença de probabilidade nestas situações parece ser contraintuitiva, já que dizer que pelo menos um deles é um menino parece ser o mesmo que dizer que o filho mais velho é menino. É sempre bom pensar duas vezes!
Um diagrama para ajudar:
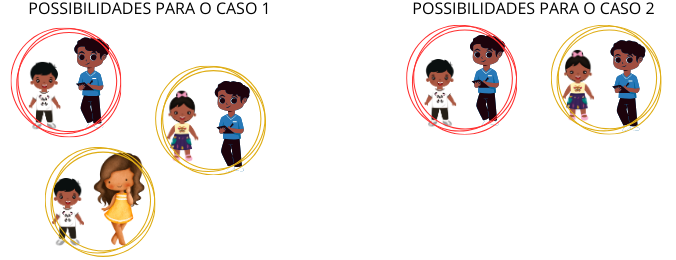
Solução elaborada pelos Moderadores do Blog.
