Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Difícil)
Daniel, Gabriel e Rafael são irmãos.
Em 2015, a idade de Rafael era o dobro da idade de Daniel e atualmente, em 2019, a soma das idades de Gabriel e Rafael é o triplo da idade de Daniel. Sabe-se que, quando Gabriel nasceu, Rafael tinha dois anos.
Em que ano a soma das idades dos três irmãos será [tex]100[/tex] anos?
Solução
Vamos adotar o ano de [tex]2015[/tex] como base para os nossos cálculos. Dessa forma, sejam [tex]D[/tex], [tex]G[/tex] e [tex]R[/tex] as respectivas idades de Daniel, Gabriel e Rafael em [tex]2015[/tex]; assim, em [tex]2019[/tex] (quatro anos depois), os irmãos terão, respectivamente, [tex]D+4[/tex], [tex]G+4[/tex] e [tex]R+4[/tex] anos.

- Sabemos que, em [tex]2015[/tex], a idade de Rafael era o dobro da idade de Daniel. Assim, [tex]R=2D[/tex], donde:
[tex]\qquad \qquad D=\dfrac{R}{2}. \qquad \qquad \textcolor{#800000}{(i)}[/tex]
Mas, quando Gabriel nasceu, Rafael tinha dois anos; assim, Rafael é dois anos mais velho que Gabriel e, portanto, [tex]R=G+2[/tex], donde
[tex]\qquad \qquad G=R-2. \qquad \qquad \textcolor{#800000}{(ii)}[/tex] - Em [tex]2019[/tex], a soma das idades de Gabriel e Rafael é o triplo da idade de Daniel. Logo, segue que:
[tex]\qquad \qquad (G+4)+(R+4)=3(D+4)[/tex]
[tex]\qquad \qquad G+R+8=3D+12[/tex]
[tex]\qquad \qquad G=3D+4-R. \qquad \qquad \textcolor{#800000}{(iii)}[/tex]
Agora, substituindo [tex]\textcolor{#800000}{(i)}[/tex] e [tex]\textcolor{#800000}{(ii)}[/tex] em [tex]\textcolor{#800000}{(iii)}[/tex], obtemos:
[tex]\qquad \qquad G\stackrel{\textcolor{#800000}{(iii)}}{=}3D+4-R[/tex]
[tex]\qquad \qquad G\stackrel{\textcolor{#800000}{(i)}}{=}3 \times \dfrac{R}{2}+4-R [/tex]
[tex]\qquad \qquad R-2\stackrel{\textcolor{#800000}{(ii)}}{=}3 \times \dfrac{R}{2}+4-R [/tex]
[tex]\qquad \qquad 2R-4=3R+8-2R [/tex]
[tex]\qquad \qquad \boxed{R=12} \, .[/tex]
Com isso, de [tex]\textcolor{#800000}{(i)}[/tex] concluímos que [tex]\boxed{D=6} \, [/tex] e de [tex]\textcolor{#800000}{(ii)}[/tex] temos que [tex]\boxed{G=10} \, .[/tex]
Já temos condições de finalizar a nossa solução. Para tanto, suponhamos que, a partir de [tex]2015[/tex], transcorram [tex]x[/tex] anos até que a soma das idades dos três irmãos seja [tex]100[/tex] anos. Dessa forma, em [tex]2015+x[/tex] as idades dos irmãos serão [tex]6+x[/tex], [tex]10+x[/tex] e [tex]12+x[/tex] anos.
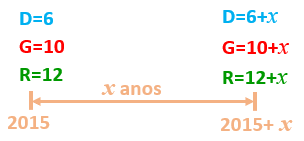
Como a soma dessas idades deverá ser [tex]100[/tex] anos, concluímos que:
[tex]\qquad \qquad (6+x)+(10+x)+(12+x)=100[/tex]
[tex]\qquad \qquad 28+3x=100[/tex]
[tex]\qquad \qquad 3x=72[/tex]
[tex]\qquad \qquad x=24[/tex] anos.
Portanto, a soma das idades de Daniel, Gabriel e Rafael será [tex]100[/tex] em [tex] \, \fcolorbox{black}{#eee0e5}{$2039$} \, .[/tex]

Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
