Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 7º ano do E. F. – Nível de dificuldade: Difícil)
Determinar de quantas maneiras podemos escrever [tex]2003 [/tex] como soma dos quadrados de dois números naturais não nulos.

Ajuda
Em várias situações é possível determinarmos a paridade de expressões envolvendo números naturais, a partir da paridade desses números, sem sequer calcular as expressões.
Particularmente, as tabelinhas abaixo ilustram situações de paridade que irão aparecer na solução deste problema:
- A soma de dois números naturais de mesma paridade é par.
- A soma de dois números naturais de paridade oposta é ímpar.
- O produto de dois números naturais só será ímpar se os dois números forem ímpares.
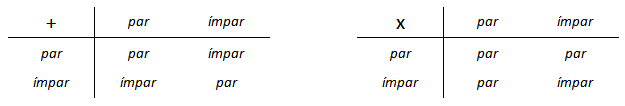
(Se precisar, visite esta Sala.)
Solução 1
Sejam [tex]x \, [/tex] e [tex] \, y[/tex] números naturais não nulos que satisfaçam as condições do problema. Assim, [tex]x^2+y^2=2003.[/tex]
- Como [tex]2003[/tex] é um número ímpar, então as propriedades elencadas na Ajuda apontam que [tex]x^2[/tex] e [tex]y^2[/tex] têm paridades opostas (veja a tabelinha da esquerda).
- Mas a tabelinha da direita mostra que o quadrado de um número mantém a sua paridade; assim, [tex]x \, [/tex] e [tex] \, y[/tex] têm paridades contrárias.
Vamos supor, sem perda de generalidade, que [tex]x[/tex] seja um número par e [tex] \, y[/tex] seja um número ímpar. Dessa forma, existem números naturais [tex]m \, [/tex] e [tex] \, n \, [/tex], com [tex] \, n\ne 0[/tex], tais que [tex] \, \boxed{x=2n} \, [/tex] e [tex] \, \boxed{y=2m+1}[/tex], donde segue que:
[tex]\qquad x^2+y^2=2003[/tex]
[tex]\qquad (2n)^2+(2m+1)^2=2003[/tex]
[tex]\qquad 4n^2+4m^2+4m+1=2003[/tex]
[tex]\qquad 4\left(n^2+m^2+m\right)+1=2003[/tex]
[tex]\qquad 4\left(n^2+m^2+m\right)=2002. \qquad \textcolor{#800000}{(i)}[/tex]
Perceba que se [tex]k=n^2+m^2+m[/tex], então de [tex]\textcolor{#800000}{(i)}[/tex] segue que [tex]2002=4k[/tex], com [tex]k\in \mathbb{N}[/tex] e com isso concluiríamos que [tex]2002[/tex] é um múltiplo de [tex]4.[/tex] Mas
[tex]\qquad \qquad \begin{array}{r}
2002 \, \end{array} \begin{array}{|r}
\, 4 \, \, \, \, \\ \hline
\end{array}[/tex]
[tex]\quad \qquad\begin{array}{r}
\qquad \textcolor{red}{2}
\end{array}\begin{array}{r}
\quad 500
\end{array}[/tex]
o que mostra que [tex]2002[/tex] NÃO é um múltiplo de [tex]4.[/tex]
Portanto, não podemos supor que existam números naturais não nulos cuja soma dos quadrados seja igual a [tex]2003[/tex], pois isso acarreta um erro.
Solução elaborada pelos Moderadores do Blog.
 |
Se você ainda não aprendeu a lidar com a álgebra, não faz mal, veja a segunda solução. |
Solução 2
Os esquemas multiplicativos abaixo nos mostram que o quadrado de um número natural não nulo termina necessariamente em [tex]0,1,4,5,6[/tex] ou [tex]9.[/tex]
|
[tex]\begin{array}{c c r c} \, \, \\ &a&\cdots&1\\ \times &a&\cdots&1\\ \hline &b&\cdots&\boxed{1} \end{array} [/tex] |
[tex] \begin{array}{c c r c} \, \, \\ &a&\cdots&2\\ \times &a&\cdots&2\\ \hline &c&\cdots&\boxed{4} \end{array} [/tex] |
[tex] \begin{array}{c c r c} \, \, \\ &a&\cdots&3\\ \times &a&\cdots&3\\ \hline &d&\cdots&\boxed{9} \end{array} [/tex] |
[tex] \begin{array}{c c r c} &&_\underline{1}&\\ &a&\cdots&4\\ \times&a&\cdots&4\\ \hline &e&\cdots&\boxed{6} \end{array} [/tex] |
|
[tex] \begin{array}{c c r c} &&_\underline{2}&\\ &a&\cdots&5\\ \times&a&\cdots&5\\ \hline &f&\cdots&\boxed{5} \end{array} [/tex] |
[tex] \begin{array}{c c r c} &&_\underline{3}&\\ &a&\cdots&6\\ \times&a&\cdots&6\\ \hline &g&\cdots&\boxed{6} \end{array} [/tex] |
[tex] \begin{array}{c c r c} &&_\underline{4}&\\ &a&\cdots&7\\ \times&a&\cdots&7\\ \hline &h&\cdots&\boxed{9} \end{array} [/tex] |
[tex] \begin{array}{c c r c} &&_\underline{6}&\\ &a&\cdots&8\\ \times&a&\cdots&8\\ \hline &l&\cdots&\boxed{4} \end{array} [/tex] |
|
[tex] \begin{array}{c c r c} &&_\underline{8}&\\ &a&\cdots&9\\ \times&a&\cdots&9\\ \hline &r&\cdots&\boxed{1} \end{array} [/tex] |
[tex] \begin{array}{c c r c} &&&\\ &a&\cdots&0\\ \times&a&\cdots&0\\ \hline &s&\cdots&\boxed{0} \end{array} [/tex] |
Dessa forma, para que a soma de dois quadrados seja [tex]2003[/tex] ([tex]x^2+y^2=2003[/tex]), um dos quadrados deve terminar em [tex]4[/tex] e o outro em [tex]9.[/tex]
Para que o quadrado de um número natural termine em [tex]9[/tex], esse número deve terminar em [tex]3[/tex] ou em [tex]7[/tex], conforme mostram os esqueminhas acima; assim, podemos listar os quadrados terminados em [tex]9[/tex] que são menores do que [tex]2003[/tex], para verificar quais diferenças [tex]2003-x^2[/tex] (que sabemos que terminam em [tex]4[/tex]) são quadrados perfeitos.
Vamos lá!
| [tex] x[/tex] | [tex]x^2[/tex] | [tex]2003-x^2[/tex] | [tex]2003-x^2[/tex] é quadrado perfeito? |
| [tex] 3[/tex] | [tex]9[/tex] | [tex]1994[/tex] | [tex]1994[/tex] não é quadrado perfeito, pois [tex]\sqrt{1994} \not\in \mathbb{N}[/tex] |
| [tex] 7[/tex] | [tex]49[/tex] | [tex]1954[/tex] | [tex]1954[/tex] não é quadrado perfeito, pois [tex]\sqrt{1954} \not\in \mathbb{N}[/tex] |
| [tex] 13[/tex] | [tex]169[/tex] | [tex]1834[/tex] | [tex]1834[/tex] não é quadrado perfeito, pois [tex]\sqrt{1834} \not\in \mathbb{N}[/tex] |
| [tex] 17[/tex] | [tex]289[/tex] | [tex]1714[/tex] | [tex]1714[/tex] não é quadrado perfeito, pois [tex]\sqrt{1714} \not\in \mathbb{N}[/tex] |
| [tex] 23[/tex] | [tex]529[/tex] | [tex]1474[/tex] | [tex]1474[/tex] não é quadrado perfeito, pois [tex]\sqrt{1474} \not\in \mathbb{N}[/tex] |
| [tex] 27[/tex] | [tex]729[/tex] | [tex]1274[/tex] | [tex]1274[/tex] não é quadrado perfeito, pois [tex]\sqrt{1274} \not\in \mathbb{N}[/tex] |
| [tex] 33[/tex] | [tex]1089[/tex] | [tex]914[/tex] | [tex]914[/tex] não é quadrado perfeito, pois [tex]\sqrt{914} \not\in \mathbb{N}[/tex] |
| [tex] 37[/tex] | [tex]1369[/tex] | [tex]634[/tex] | [tex]634[/tex] não é quadrado perfeito, pois [tex]\sqrt{634} \not\in \mathbb{N}[/tex] |
| [tex] 43[/tex] | [tex]1849[/tex] | [tex]154[/tex] | [tex]154[/tex] não é quadrado perfeito, pois [tex]\sqrt{154} \not\in \mathbb{N}[/tex] |
| [tex] 47^2=2209 \gt 2003[/tex] | |||
Assim, não existem números naturais não nulos [tex]x \, [/tex] e [tex] \, y[/tex] tais que [tex]x^2+y^2=2003.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
